题目内容
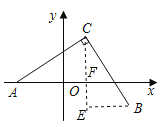
【题目】如图,∠ACB=90°,AC=BC,点C(2,4)、A(﹣4,0),则点B的坐标是______.

【答案】(6,﹣2)
【解析】
如图,过点C作CF⊥AO,过点B作BE⊥CF,通过证明△ACF≌△CBE,可得BE=CF=4,CE=AF=6,即可求解.
如图,过点C作CF⊥AO,过点B作BE⊥CF,
∵点C(2,4)、A(﹣4,0),
∴CF=4,OF=2,AO=4,AF=6,
∵∠ACB=90°,
∴∠ACF+∠BCF=90°,且∠ACF+∠CAF=90°,
∴∠BCF=∠CAF,且AC=BC,∠AFC=∠CEB=90°,
∴△ACF≌△CBE(AAS)
∴BE=CF=4,CE=AF=6,
∴EF=2,
∴点B(6,﹣2),
故答案为:(6,﹣2).

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
【题目】随机抽取某市一年(以365天计)中的30天的日平均气温状况统计如下:温度(![]() )
)
温度( | 10 | 14 | 18 | 22 | 26 | 30 | 32 |
天数 | 3 | 5 | 5 | 7 | 6 | 2 | 2 |
请根据上述数据回答下列问题:
(1)估计该城市年平均气温大约是多少?
(2)上表中的温度数据的中位数是_______众数是_________;
(3)计算该城市一年中约有几天的日平均气温为![]() ?
?





