题目内容
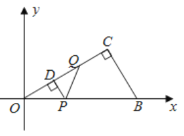
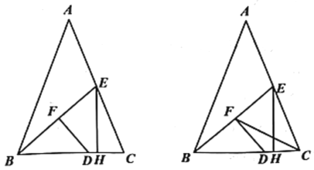
【题目】已知:如图1,△ABC中,AB=AC,BC=6,BE为中线,点D为BC边上一点;BD=2CD,DF⊥BE于点F,EH⊥BC于点H.
(1)CH的长为_____;
(2)求BF·BE的值:
(3)如图2,连接FC,求证:∠EFC=∠ABC.
【答案】(1)1.5(2)18(3)见解析
【解析】
(1)根据BE是AC边上的中线,可以判断出E点是AC的中点,过A作BC的垂线,垂足为G,可以得出EH∥AG,再根据平行线分线段成比例计算即可.
(2)根据BD和CD的关系计算出CD、BD的长,然后结合第(1)问中CH的长,计算出BH的长,根据三角形相似的判定定理求出![]() ,再根据相似三角形的性质定理列出关于BF,BE的比例关系式,化简求解即可.
,再根据相似三角形的性质定理列出关于BF,BE的比例关系式,化简求解即可.
(3)过A作 AM∥BC 交BE延长线于 M,根据平行线的性质定理得出相等角,通过三角形全等的判定定理推出![]() ,得出AM的长度,以及BM和BE的关系,然后通过AM,BC,BF,BM的数量关系,列出比例关系式,再结合
,得出AM的长度,以及BM和BE的关系,然后通过AM,BC,BF,BM的数量关系,列出比例关系式,再结合 ![]() ,根据相似三角形的判定定理得出
,根据相似三角形的判定定理得出![]() ,从而得出
,从而得出![]() ,然后通过等量代换即可求证
,然后通过等量代换即可求证![]() .
.
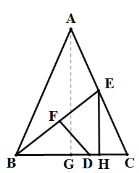
解:作AG⊥BC于G,
∵AB=AC,BC=6,
∴CG=3,
∵AE=EC,
EH⊥BC,
∴EH∥AG,
![]()
![]()
(2)![]()
![]()
![]()
![]()
![]() .
.
![]() ,
,![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
(3)过A作 AM∥BC 交BE延长线于 M

![]()
![]() ,
,
![]() .
.
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案【题目】某校为了解学生课外阅读情况,就学生每周阅读时间随机调查了部分学生,调查结果按性别整理如下:
女生阅读时间人数统计表
阅读时间 | 人数 | 占女生人数百分比 |
| 4 |
|
|
|
|
| 5 |
|
| 6 |
|
| 2 |
|
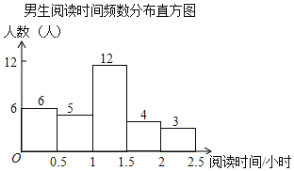
根据图表解答下列问题:
(1)在女生阅读时间人数统计表中,![]() ,
,![]() ;
;
(2)此次抽样调查中,共抽取了 名学生,学生阅读时间的中位数在 时间段;
(3)从阅读时间在2~2.5小时的5名学生中随机抽取2名学生参加市级阅读活动,恰好抽到男女生各一名的概率是多少?
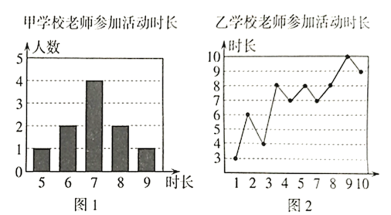
【题目】甲、乙两所学校选派相同人数的老师参加志愿者活动,參加活动时长分别被制成下列两个统计图,根据以上信息,整理分析数据如下表:
平均时间/小时 | 中位数/小时 | 众数/小时 | 方差/小时 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
![]() 求出表格中
求出表格中![]() 的值.
的值.
![]() 分别运用表中的统计量,简要分析这两所学校参加志愿者活动的时长,若选其中一所学校作为志愿推广学校,你认为应该选哪所?
分别运用表中的统计量,简要分析这两所学校参加志愿者活动的时长,若选其中一所学校作为志愿推广学校,你认为应该选哪所?