题目内容
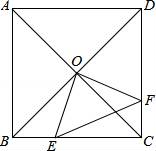
【题目】如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为( )
A.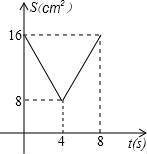
B.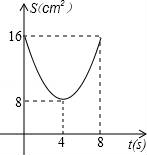
C.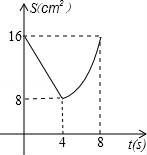
D.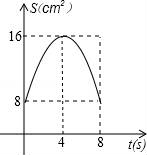
【答案】B.
【解析】
试题分析:由点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,得到BE=CF=t,则CE=8﹣t,再根据正方形的性质得OB=OC,∠OBC=∠OCD=45°,然后根据“SAS”可判断△OBE≌△OCF,所以S△OBE=S△OCF,这样S四边形OECF=S△OBC=16,于是S=S四边形OECF﹣S△CEF=16﹣![]() (8﹣t)t,然后配方得到S=
(8﹣t)t,然后配方得到S=![]() (t﹣4)2+8(0≤t≤8),∴s(cm2)与t(s)的函数图象为抛物线一部分,顶点为(4,8),自变量为0≤t≤8.故选:B.
(t﹣4)2+8(0≤t≤8),∴s(cm2)与t(s)的函数图象为抛物线一部分,顶点为(4,8),自变量为0≤t≤8.故选:B.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目