题目内容
若方程a|x|=x+a (a>0且a≠±1) 有两个解,则a的取值范围是
- A.0<a<1
- B.0<a<1或a>1
- C.a>1
- D.不存在这样的a
C
分析:根据方程a|x|=x+a(a>0且a≠±1)有两个解,可得知有一个正根与一个负根,然后分类x的取值范围即可求解.
解答:由方程a|x|=x+a (a>0且a≠±1) 有两个解,可得知有一个正跟与一个负根,
当x>0时,解方程得:x=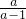 (a>0且a≠±1),则a>1;
(a>0且a≠±1),则a>1;
当x<0时,解方程得:x=-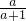 (a>0且a≠±1),则a>-1.
(a>0且a≠±1),则a>-1.
综上所述,∴a>1.
故选C.
点评:本题考查了含绝对值符号的一元一次方程,难度适中,关键是正确分类讨论x的取值范围.
分析:根据方程a|x|=x+a(a>0且a≠±1)有两个解,可得知有一个正根与一个负根,然后分类x的取值范围即可求解.
解答:由方程a|x|=x+a (a>0且a≠±1) 有两个解,可得知有一个正跟与一个负根,
当x>0时,解方程得:x=
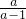 (a>0且a≠±1),则a>1;
(a>0且a≠±1),则a>1;当x<0时,解方程得:x=-
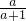 (a>0且a≠±1),则a>-1.
(a>0且a≠±1),则a>-1.综上所述,∴a>1.
故选C.
点评:本题考查了含绝对值符号的一元一次方程,难度适中,关键是正确分类讨论x的取值范围.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
若方程x2-3x-2=0的两实数根为x1,x2,则
+
的值为( )
| 1 |
| x1 |
| 1 |
| x2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
若方程
=
+
有增根,则增根可能为( )
| 3 |
| x-2 |
| a |
| x |
| 4 |
| x(x-2) |
| A、0 | B、2 | C、0或2 | D、1 |
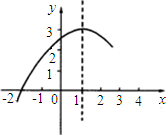 图象回答下列问题:
图象回答下列问题: