题目内容
【题目】如图,△ABC是边长为a的等边三角形,P是△ABC内的任意一点,过点P作EF∥AB分别交AC,BC于点E,F,过点P作GH∥BC分别交AB,AC于点G,H,过点P作MN∥AC分别交AB,BC于点M,N,猜想EF+GH+MN的值是多少.其值是否随点P位置的改变而改变?并说明理由.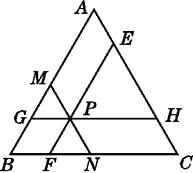
【答案】解:EF+GH+MN=2a,EF+GH+MN的值不随点P位置的改变而改变.理由如下:
∵△ABC是等边三角形,∴∠A=∠B=∠C=60°.
∵GH∥BC,
∴∠AGH=∠B=60°,∠AHG=∠C=60°.
∴△AGH是等边三角形,
∴GH=AG=AM+MG.①
同理△BMN是等边三角形,
∴MN=MB=MG+GB.②
∵MN∥AC,EF∥AB,
∴四边形AMPE是平行四边形,
∴PE=AM.
同理可证四边形BFPG是平行四边形,
∴PF=GB.
∴EF=PE+PF=AM+GB.③
由①②③,得
EF+GH+MN=(AM+GB)+(AM+MG)+(MG+GB)=2(AM+MG+GB)=2AB=2a
【解析】根据已知条件△ABC是等边三角形及GH∥BC、MN∥AC,证明△AGH和△BMN是等边三角形,从而得出GH=AG=AM+MG,MN=MB=MG+GB,再证明四边形AMPE和四边形BFPG是平行四边形,得出PE=AM,PF=GB,然后通过等量代换就可得出EF+GH+MN=2AB即可。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
