题目内容
【题目】现有一生产季节性产品的企业,有两种营销方案,经测算:方案一,一年中获得的每月利润y(万元)和月份x的关系为![]() ;方案二,一年中获得的每月利润y(万元)与月份x的关系为
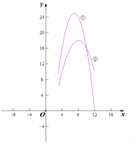
;方案二,一年中获得的每月利润y(万元)与月份x的关系为![]() .两个函数部分图象如图所示:
.两个函数部分图象如图所示:

(1)请你指出:方案一,月利润对应的图象是 ;方案二,月利润对应的图象是 ;(填序号)
(2)该企业一年中月利润最高可达 万元;
(3)生产季节性产品的企业,当它的产品无利润时就会立即停 产,企业原计划全年使用营销方案二进行销售,
则①该企业一年中应停产的月份是 ;
②为了使全年能获得更高利润,企业应该如何改进其营销方案,使全年总利润最高?并算出全年最高总利润比原计划多多少?
【答案】(1) ②, ①;(2)25;(3) ①1月,2月 ,12月; ②从2月份到10月份选择方案二,11月份和12月份选择方案一,可以使全年总利润最高;去年最高总利润比原计划多23.5万元.
【解析】试题分析: (1)将方案一和方案二的解析式化为顶点式,即可得到相应的最大值,再结合函数图象即可解答本题;
(2)将方案一和方案二的解析式化为顶点式,即可得到相应的最大值,本题得以解决;
(3)①解答本题只要算出方案一和方案二都等于0的情况,即可得到哪个月份需要停产;
②解答本题只要算出方案一不小于方案二的情况,即可得到最优方案,从而可以得到去年最高总利润比原计划多多少.
试题解析:
(1)方案一:y=0.5x2+8x14=0.5(x216x)14=0.5(x8)2+18,y的最大值是18,
方案二:y=x2+14x24=(x7)2+25,y的最大值是25,
∴方案一月利润对应的函数图象是②,方案二对应的图象是①,
故答案为:②,①;
(2)∵方案一:y=0.5x2+8x14=0.5(x216x)14=0.5(x8)2+18,y的最大值是18,
方案二:y=x2+14x24=(x7)2+25,y的最大值是25,
∴该企业一年中月利润最高可达25万元,
故答案为:25;
(3)①将y=0代入y=0.5x2+8x14,得x=2或x=14,故方案一停产的月份是1月份、2月份;
将y=0代入y=x2+14x24,得x=2或x=12,故方案二停产的月份是1月份、2月份、12月份;
故答案为:方案一是1月份和2月份,方案二是1月份、2月份、12月份;
②令﹣0.5x2+8x﹣14=﹣x2+14x﹣24,得x=2或x=10,
∴从2月份到10月份选择方案二,11月份和12月份选择方案一,可以使全年总利润最高;
∴去年最高总利润比原计划多的钱数是:
(-0.5×112+8×11﹣14)+(﹣0.5×122+8×12﹣14)=23.5(万元),
即去年最高总利润比原计划多23.5万元.

 阅读快车系列答案
阅读快车系列答案