题目内容
【题目】如图,等边![]() 的边长为
的边长为![]() ,动点P从点A出发,以每秒
,动点P从点A出发,以每秒![]() 的速度,沿
的速度,沿![]() 的方向运动,到达点C时停止,设运动时间为x(s),则y关于x的函数的图象大致是( )
的方向运动,到达点C时停止,设运动时间为x(s),则y关于x的函数的图象大致是( )

A.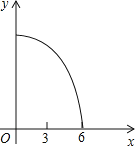 B.
B.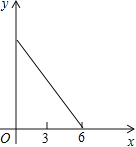 C.
C.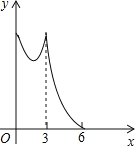 D.
D.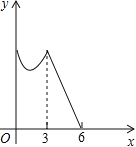
【答案】C
【解析】
过C作CD⊥AB,则分开两段函数进行讨论:①当点P从A到B时;②当点P从B到C时,分别求出解析式,即可得到答案.
解:过C作CD⊥AB,
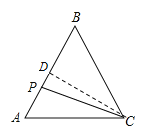
则AD=1.5cm,CD=![]() cm,点P在AB上时,AP=xcm,PD=|1.5-x|cm,
cm,点P在AB上时,AP=xcm,PD=|1.5-x|cm,
∴y=PC2=(![]() )2+(1.5-x)2=x2-3x+9(0≤x≤3),
)2+(1.5-x)2=x2-3x+9(0≤x≤3),
该函数图象是开口向上的抛物线;
②当3<x≤6时,即点P在线段BC上时,PC=(6-x)cm(3<x≤6);
则y=(6-x)2=(x-6)2(3<x≤6),
∴该函数的图象是在3<x≤6上的抛物线;
故选择:C.

练习册系列答案
相关题目