题目内容
【题目】如图，矩形ABCD的顶点A，B在圆上，BC，AD分别与该圆相交于点E，F，G是弧AF的三等分点（弧AG＞弧GF)，BG交AF于点H．若弧AB的度数为30°，则∠GHF等于( )
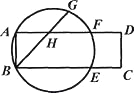
A. 40° B. 45° C. 55° D. 80°
【答案】A
【解析】连接BF，取BF中点O，连接OA、OG，根据90度的圆周角所对的弦是直径可得BF为⊙O的直径，再根据
的度数是30°，可知
的度数为150°，继而由已知G是的三等分点（
)，可得到∠ABG =50°，从而即可得到∠GHF的度数.
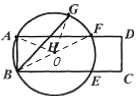
连接BF，取BF中点O，连接OA、OG，
∵四边形ABCD是矩形，∴∠BAD=90°，∴BF为⊙O的直径，
∵的度数是30°，∴的度数为150°，
∵G是的三等分点（)，
∴∠FOG=50°，∠AOG=100°，
∴∠ABG=
∠AOG=50°，
∴∠AHB=90°-∠ABG=40°，
∴∠GHF=∠AHB=40°，
故选A.
练习册系列答案
名校课堂系列答案
相关题目
