题目内容
【题目】如图,抛物线y=ax2+bx过点B(1,﹣3),对称轴是直线x=2,且抛物线与x轴的正半轴交于点A.
(1)求抛物线的解析式,并根据图象直接写出当y≤0时,自变量x的取值范图;
(2)在第二象限内的抛物线上有一点P,当PA⊥BA时,求△PAB的面积.

【答案】(1)抛物线的解析式为y=x2﹣2x,自变量x的取值范图是0≤x≤2;(2)△PAB的面积=![]() .
.
【解析】(1)将函数图象经过的点B坐标代入的函数的解析式中,再和对称轴方程联立求出待定系数a和b;
(2)如图,过点B作BE⊥x轴,垂足为点E,过点P作PE⊥x轴,垂足为F,设P(x,x2-2x),证明△PFA∽△AEB,求出点P的坐标,将△PAB的面积构造成长方形去掉三个三角形的面积.
(1)由题意得,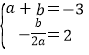 ,解得
,解得![]() ,
,
∴抛物线的解析式为y=x2-2x,
令y=0,得x2-2x=0,解得x=0或2,
结合图象知,A的坐标为(2,0),
根据图象开口向上,则y≤0时,自变量x的取值范图是0≤x≤2;
(2)如图,过点B作BE⊥x轴,垂足为点E,过点P作PE⊥x轴,垂足为F,
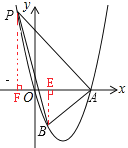
设P(x,x2-2x),
∵PA⊥BA
∴∠PAF+∠BAE=90°,
∵∠PAF+∠FPA=90°,
∴∠FPA=∠BAE
又∠PFA=∠AEB=90°
∴△PFA∽△AEB,
∴![]() ,即
,即![]() ,
,
解得,x= ![]() ,
,
∴x2-2x=![]() .
.
∴点P的坐标为(![]() ,
,![]() ),
),
∴△PAB的面积=|-![]() 2|×|
2|×|![]() (3)|-
(3)|-![]() ×|
×|![]() 2|×
2|×![]() -
-![]() ×|-
×|-![]() 1|×|
1|×|![]() (3)|-
(3)|- ![]() ×|2-1|×|0-(-3)|=
×|2-1|×|0-(-3)|=![]() .
.

练习册系列答案
相关题目