题目内容
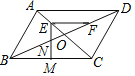
【题目】如图,将矩形纸片ABCD折叠,使边AD落在对角线BD上,折痕为DE,且A点落在对角线F处.若AD=3,CD=4,则AE的长为( )
A. ![]() B. 1 C. 2 D.
B. 1 C. 2 D. ![]()
【答案】A
【解析】分析: 根据矩形对边相等可得AB=CD,再利用勾股定理列式求出BD,根据翻折的性质可得DF=AD,EF=AE,∠DFE=∠A=90°,然后求出BF,设AE=x,表示出BE,在Rt△BEF中,利用勾股定理列方程求解即可.
详解: 在矩形ABCD中,AB=CD=4,
由勾股定理得,BD=![]() =
=![]() =5,
=5,
∵矩形纸片ABCD折叠,边AD落在对角线BD上,A点落在对角线F处
∴DF=AD=3,EF=AE,∠DFE=∠A=90°,
∴BF=BD-DF=5-3=2,
设AE=x,则BE=4-x,
在Rt△BEF中,由勾股定理得,BF2+EF2=BE2,
即22+x2=(4-x)2,
解得x=![]() ,
,
即AE的长为![]() .
.
故选A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目