题目内容
【题目】已知:如图∠ABC=∠ADC=90°,M,N分别是AC、BD的中点.
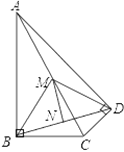
(1)求证:MN⊥BD.
(2)若∠BAD=45°,连接MB、MD,判断△MBD的形状,并说明理由.
【答案】(1)详见解析;(2)等腰直角三角形,理由详见解析.
【解析】
(1)由直角三角形斜边中线的性质可得BM=![]() AC,DM=
AC,DM=![]() AC,即可证明BM=DM,由N是BD的中点,根据等腰三角形“三线合一”的性质即可得结论;(2)根据直角三角形斜边中线的性质可得AM=
AC,即可证明BM=DM,由N是BD的中点,根据等腰三角形“三线合一”的性质即可得结论;(2)根据直角三角形斜边中线的性质可得AM=![]() AC=BM,即可证明∠BAM=∠ABM,利用三角形外角性质可得∠MBC=2∠BAM,同理可得∠DMC=2∠DAM,利用角的和差关系可得∠BDM=90°,由BM=DM即可得出△MBD为等腰直角三角形.
AC=BM,即可证明∠BAM=∠ABM,利用三角形外角性质可得∠MBC=2∠BAM,同理可得∠DMC=2∠DAM,利用角的和差关系可得∠BDM=90°,由BM=DM即可得出△MBD为等腰直角三角形.
(1)∵∠ABC=∠ADC=90°,M,N分别是AC、BD的中点,
∴BM=![]() AC,DM=
AC,DM=![]() AC,
AC,
∴BM=DM,
∵N是BD的中点,
∴MN⊥BD.
(2)等腰直角三角形,理由:
∵M是AC的中点,∠ABC=90°,
∴AM=![]() AC=BM,
AC=BM,
∴∠BAM=∠ABM,
∴∠BMC=2∠BAM,
同理可得∠DMC=2∠DAM,
又∵∠BAD=45°,
∴∠BDM=∠BMC+∠DMC=2(∠BAM+∠DAM)=2∠BAD=90°,
又∵BM=DM,
∴△BDM是等腰直角三角形.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目