Question

【题目】如图，在△ABC中，∠C＝90°，D，F是AB边上的两点，以DF为直径的⊙O与BC相交于点E，连接EF，∠OFE＝∠A.

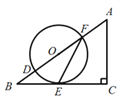
(1)求证：BC是⊙O的切线；

(2)若sinB＝，求∠FEC。

Answer 1

【答案】（1）证明见解析；（2）60°

【解析】试题分析：（1）首先连接OE，由在△ABC中，∠C=90°，FG⊥BC，可得FG∥AC，又由∠OFE=∠A，易得EF平分∠BFG，继而证得OE∥FG，证得OE⊥BC，则可得BC是⊙O的切线；

（2）由sinB=得，∠B＝30°，从而∠A=60°，由∠OFE＝∠A得∠OFE=30°

故得∠FEC=60°

试题解析：（1）连接OE，

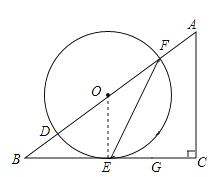
∵在△ABC中，∠C=90°，FG⊥BC，

∴∠BGF=∠C=90°，

∴FG∥AC，

∴∠OFG=∠A，

∴∠OFE=∠OFG，

∴∠OFE=∠EFG，

∵OE=OF，

∴∠OFE=∠OEF，

∴∠OEF=∠EFG，

∴OE∥FG，

∴OE⊥BC，

∴BC是⊙O的切线；

（2）在RtΔABC中，sinB=

∴∠B=30°

∴∠A=60°

∵∠OFE=∠A，

∴∠OFE=30°

∴∠FEC=30°+30°=60°