Question

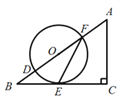
【题目】如图，以Rt△ABC的三边为斜边分别向外作等腰直角三角形．若斜边AB= ，则图中阴影部分的面积为（ ）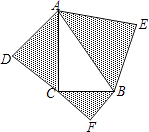
A.1
B.
C.
D.

Answer 1

【答案】A
【解析】解：在Rt△ADC中，AC2=AD2+DC2 ， AD=DC， ∴AC2=2AD2 ，
∴DC=AD= AC，
同理；CF=BF= BC，BE=AE= AB，
在Rt△ABC中，AB2=AC2+BC2 ， AB= ，
S阴影=S△ADC+S△BFC+S△AEB= DCAD+ CFBF+ AEBE，
= （AC2+BC2+AB2）
= （AB2+AB2）
= ×2AB2
= AB2
= ×2
=1；
故选：A．
【考点精析】本题主要考查了勾股定理的概念的相关知识点，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题．