��Ŀ����
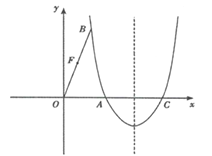
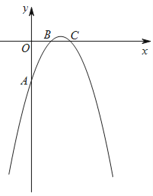
����Ŀ����֪���κ���y����x2��ax��b��ͼ����y�ύ�ڵ�A(0����2)����x�ύ�ڵ�B(1��0)�͵�C��D(m��0)(m��2)��x����һ�㣮
(1)����κ����Ľ���ʽ��
(2)��E�ǵ��������ڵ�һ�㣬���Ե�DΪֱ�Ƕ����Rt��CDE����A��O��BΪ��������������ƣ����E����(�ú�m�Ĵ���ʽ��ʾ)��
(3)��(2)�������£����������Ƿ����һ��F��ʹ���ı���BCEFΪƽ���ı��Σ������ڣ��������F�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2��
����2��![]() ��
��![]() ����3�����ڣ�
����3�����ڣ�![]()
�������������������1������A��1��0����B��2��0����C��0��-2��������κ���y=ax2+bx+c�У��з�������a��b��c���ɣ�
��2����ΪD��O�ֱ�Ϊ����ֱ�������εĶ��㣬�ɷ�Ϊ��EDB�ס�AOC����BDE�ס�AOC����������������Ʊ���ED��ȷ��E�����ꣻ
��3�������������ϴ���һ��F��ʹ���ı���ABEFΪƽ���ı��Σ�EF=AB=1����F�ĺ�����Ϊm-1����Ϊ�ٵ���E1������Ϊ��m�� ![]() ��ʱ����F1������Ϊ��m-1��
��ʱ����F1������Ϊ��m-1�� ![]() �����ڵ���E2������Ϊ��m��4-2m��ʱ����F2������Ϊ��m-1��4-2m��������������ֱ���������߽���ʽ��m��ֵ��ȷ��F������꣮
�����ڵ���E2������Ϊ��m��4-2m��ʱ����F2������Ϊ��m-1��4-2m��������������ֱ���������߽���ʽ��m��ֵ��ȷ��F������꣮
���������(1)�������⣬��![]() ����ã�a��3��b����2
����ã�a��3��b����2
![]() ��
��
��2����y��0ʱ���У�x2��3x��2��0����ã�x1��1��x2��2����OC��2.
�������AO��2��BO��1��CD��m��2.
��CDE�ס�AOC��ʱ����AO��CD��BO��DE��
�ࡡ2��(m��2)��1��DE.����DE��![]() .
.
�ߵ�![]() �ڵ������ޣ���E1��m��
�ڵ������ޣ���E1��m�� ![]() ����
����
����DEC�ס�AOC��ʱ����AO��ED��BO��CD��
��2��DE��1��(m��2).����DE��2m��4.
�ߵ�![]() �ڵ������ޣ���E2��m��4-2m��.
�ڵ������ޣ���E2��m��4-2m��.
��3�������������ϴ���һ��F��ʹ���ı���BCEFΪƽ���ı��Σ���EF��BC��1��
��F�ĺ�����Ϊm��1��
����![]() ������Ϊ
������Ϊ![]() ʱ����
ʱ����![]() ������Ϊ
������Ϊ![]()
�ߵ�![]() �������ߵ�ͼ���ϣ�
�������ߵ�ͼ���ϣ�
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ����ȥ����
����ȥ����
��![]() .
.
����![]() ������Ϊ
������Ϊ![]() ʱ����
ʱ����![]() ������Ϊ
������Ϊ![]() .
.
�ߵ�![]() �������ߵ�ͼ���ϣ�
�������ߵ�ͼ���ϣ�
��![]() ��
��
��![]() ��
��
��![]() ����
����![]() ����ȥ����
����ȥ����![]() ��
��
��![]() ��
��
��ʹ���ı���BCEFΪƽ���ı��εĵ�F������Ϊ![]() ��
��![]() .
.