题目内容
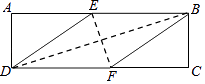
【题目】如图，平行四边形ABCD中，AB＝4，BC＝2.若把它放在平面直角坐标系中，使AB在x轴上，点C在y轴上，如果点A的坐标为(－3，0)，求点B，C，D的坐标．
【答案】点B，C，D的坐标分别为(1，0)，(0，
)和(－4，)．
【解析】首先根据AB的长度和点A的坐标得出点B的坐标，根据BC和OB的长度以及直角三角形的勾股定理求出OC的长度，从而得出点C的坐标，根据平行四边形的性质得出点D的坐标．
∵AB＝4，点A的坐标为(－3，0)， 设点B的坐标为(b，0)，
则b－(－3)＝b＋3＝4，∴b＝1，∴点B的坐标为(1，0)． 设点C的坐标为(0，c)，
由OB＝1，BC＝2，得OC＝
＝
＝
，∴点C的坐标为(0，)．
∵CD∥AB，∴点D的坐标为(－4，)．
∴点B，C，D的坐标分别为(1，0)，(0，)和(－4，)．
练习册系列答案
相关题目
