题目内容
【题目】如图,已知E、F分别为平行四边形ABCD的对边AD、BC上的点,且DE=BF,EM⊥AC于M,FN⊥AC于N,EF交AC于点O,
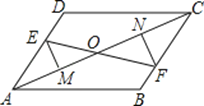
求证:(1)EM=FN;
(2)EF与MN互相平分.
【答案】(1)答案见解析;(2)答案见解析
【解析】试题分析:(1)由平行四边形的性质得出AD∥BC,AD=BC,得出∠EAM=∠FCN,AE=CF,由AAS证明△AEM≌△CFN,得出对应边相等即可;
(2)连接EN、FM,求出EM=FN,EM∥FN,得出平行四边形EMFN,根据平行四边形的性质得出即可.
证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,
∴∠EAM=∠FCN,
∵DE=BF,
∴AE=CF,∵EM⊥AC于M,FN⊥AC于N,∴∠AME=∠CNF=90°,
在△AEM和△CFN中,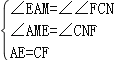 ,
,
∴△AEM≌△CFN(AAS),
∴EM=FN;
(2)连接EN、FM,如图所示:
∵EM⊥AC,FN⊥AC,
∴∠AME=∠EMN=∠FNC=∠FNM=90°,
∴EM∥FN,
又∵由(1)得EM=FN,
∴四边形EMFN是平行四边形,
∴EF与MN互相平分.


练习册系列答案
相关题目