题目内容
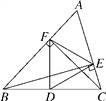
【题目】如图,在△ABC中,∠A=60°,BE⊥AC,垂足为E,CF⊥AB,垂足为F,点D是BC的中点.
(1)求证:DE=DF;
(2)试猜想△DEF是不是等边三角形?如果是,请加以证明;如果不是,请说明理由.
【答案】(1)证明见解析;(2)△DEF是等边三角形.理由见解析.
【解析】
(1)由DE和DF都是以BC为斜边的直角三角形BCF和直角三角形BCE的中线,所以相等;
(2)由等腰三角形性质得∠EDC=180°-2∠DCE,∠BDF=180°-2∠ABD,
由平角定义得∠FDE=180°-∠EDC-∠BDF=180°-(180°-2∠DCE)-(180°-2∠ABD)=2(∠DCE+∠ABD)-180°=2×(180°-∠A)-180°=60°,由(1)知DE=DF,根据等边三角形判定可得.
(1)证明:在Rt△BFC中,
∵DF为斜边BC上的中线,
∴DF=![]() BC.
BC.
同理可得DE=![]() BC,
BC,
∴DE=DF.
(2)解:△DEF是等边三角形.理由如下:
由(1)知DE=![]() BC=CD,
BC=CD,
∴∠EDC=180°-2∠DCE.
同理∠BDF=180°-2∠ABD,
∴∠FDE=180°-∠EDC-∠BDF=180°-(180°-2∠DCE)-(180°-2∠ABD)=2(∠DCE+∠ABD)-180°=2×(180°-∠A)-180°=60°.
由(1)知DE=DF,
∴△DEF是等边三角形.

练习册系列答案
相关题目