题目内容
【题目】解答题 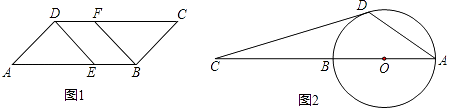
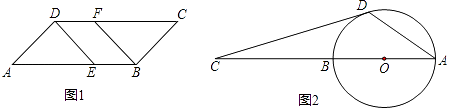
(1)如图1,在平行四边形ABCD中,已知点E在AB上,点F在CD上,且AE=CF.求证:DE=BF;
(2)如图2,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,求∠CDA的度数.
【答案】
(1)证明:∵四边形ABCD是ABCD,
∴AB∥CD,AB=CD,
∵AE=CF,
∴BE=DF,
∴四边形BEDF是平行四边形,
∴DE=BF;
(2)解:连接OD,
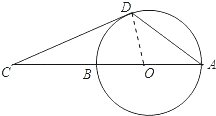
则∠ODC=90°,∠COD=70°;
∵OA=OD,
∴∠ODA=∠A= ![]() ∠COD=35°,
∠COD=35°,
∴∠CDA=∠CDO+∠ODA=90°+35°=125°.
【解析】(1)根据平行四边形的性质可证AB∥CD,AB=CD,又由已知可证BE=DF,即证四边形BEDF是平行四边形,故DE=BF;(2)连接OD,构造直角三角形,利用OA=OD,可求得∠ODA=35°,从而根据∠CDA=∠CDO+∠ODA计算求解.
【考点精析】关于本题考查的平行四边形的性质和切线的性质定理,需要了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能得出正确答案.

练习册系列答案
相关题目