题目内容
【题目】问题发现:数学兴趣小组在活动时,老师提出了这样一个问题:如图①,在Rt△ABC中,∠BAC=90°,BC=10,AD是BC边上的中线,求AD的长度.小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使DE=AD,则AD=![]() AE
AE

在△ADC和△EDB中

∴△ADC≌△EDB
∴∠DBE=∠DCA,BE=AC
∴BE∥AC
∴∠EBA+∠BAC=180°
∵∠BAC=90°
∴∠EBA=90°
在△EBA和△CAB中

∴△EBA≌△CAB
∴AE=BC
∵BC=10
∴AD=![]() AE=
AE=![]() BC=5
BC=5
(1)若将上述问题中条件“BC=10”换成“BC=a”,其他条件不变,则可得AD= .
从上得到结论:直角三角形斜边上的中线,等于斜边的一半.
(感悟)解题时,条件中若出现“中点”“中线”等字样,可以考虑延长中线构造全等三角形进而求解.
问题解决:(2)如图②,在四边形ABCD中,AD∥BC,∠D=90°,M是AB的中点.若CM=6.5,BC+CD+DA=17,求四边形ABCD的面积.
问题拓展:(3)如图③,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,∠DFE与∠AEF的度数满足数量关系:∠DFE=k∠AEF,求k的值.
【答案】(1)![]() ;(2)30;(3)k=3
;(2)30;(3)k=3
【解析】
问题发现(1):证明△ADC≌△EDB(SAS),可得∠DBE=∠DCA,BE=AC,证明△EBA≌△CAB(SAS),可得出AE=BC,则可求出答案;
问题解决:(2)延长CM、DA交于点E.根据AAS可以证明△AME≌△BMC,则ME=MC=6.5,AE=BC;根据BC+CD+DA=17,得DE+DC=17①,根据勾股定理,得DE2+DC2=CE2=169②,联立求得DECD的值,即可求得答案;
问题拓展:(3)连接CF并延长交BA的延长线于G,先证明CF=GF,再由直角三角形斜边上的中线性质可证明EF=CF,得出∠G=∠FEG,再证明AF=AG,得出∠G=∠AFG=∠DFC,即可求出答案.
解:(1)问题发现:
延长AD到E,使DE=AD,则AD=![]() AE,
AE,

在△ADC和△EDB中,
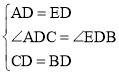 ,
,
∴△ADC≌△EDB(SAS),
∴∠DBE=∠DCA,BE=AC,
∴BE∥AC,
∴∠EBA+∠BAC=180°,
∵∠BAC=90°
∴∠EBA=90°
在△EBA和△CAB中,
 ,
,
∴△EBA≌△CAB(SAS)
∴AE=BC,
∵BC=a,
∴AD=![]() AE=
AE=![]() BC=
BC=![]() .
.
故答案为:![]() .
.
问题解决:(2)
如图②,延长CM、DA交于点E.

∵AD∥BC,
∴∠MAE=∠B,∠E=∠BCM.
又AM=BM,
∴△AME≌△BMC(AAS).
∴ME=MC=6.5,AE=BC.
又BC+CD+DA=17,∠D=90°,
∴DE+DC=17①,DE2+DC2=CE2=169②.
∴DECD=![]() [(DE+DC)2﹣DE2﹣DC2]=60.
[(DE+DC)2﹣DE2﹣DC2]=60.
∴四边形ABCD的面积为S=![]() DECD=30.
DECD=30.
问题拓展:(3)
连接CF并延长交BA的延长线于G,如图③所示:

∵四边形ABCD是平行四边形,
∴AB∥CD
∵F是AD的中点,
∴CF=GF,
∵CE⊥AB,
∴∠CEG=90°,
∴EF=![]() CG=CF=GF,
CG=CF=GF,
∴∠G=∠FEG,
∵AD∥BC,CF=GF,
∴AG=AB,
∴AF=AG,
∴∠G=∠AFG=∠DFC,
∵∠CFE=∠G+∠AEF,
∴∠DFE=∠CFE+∠DFC=3∠AEF,
∵∠DFE=k∠AEF,
∴k=3.

 名校课堂系列答案
名校课堂系列答案【题目】已知某品牌的饮料有大瓶装与小瓶装之分.某超市花了3800元购进一批该品牌的饮料共1000瓶,其中大瓶和小瓶饮料的进价及售价如下表所示:
大瓶 | 小瓶 | |
进价(元/瓶) | 5 | 2 |
售价(元/瓶) | 7 | 3 |
(1)该超市购进大瓶和小瓶饮料各多少瓶?
(2)在大瓶饮料售出200瓶,小瓶饮料售出100瓶后,商家决定将剩下的小瓶饮料的售价降低0.5元销售,并把其中一定数量的小瓶饮料作为赠品,在顾客一次性购买大瓶饮料时,每满2瓶就送1瓶小瓶饮料,送完即止.超市要使这批饮料售完后获得的利润不低于1250元,那么小瓶饮料作为赠品最多只能送出多少瓶?



