题目内容
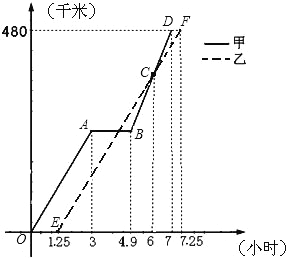
【题目】(1)已知![]() 是直角三角形,
是直角三角形,![]() ,
,![]() ,直线l经过点
,直线l经过点![]() ,分别从点
,分别从点![]() 、
、![]() 向直线l作垂线,垂足分别为
向直线l作垂线,垂足分别为![]() 、
、![]() .当点
.当点![]() ,
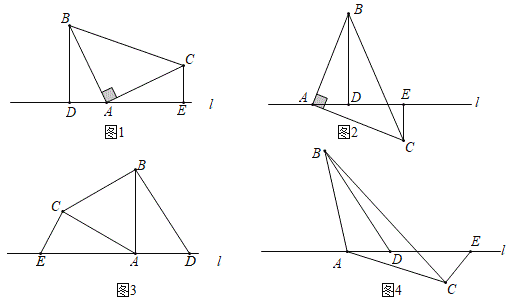
,![]() 位于直线l的同侧时(如图
位于直线l的同侧时(如图![]() ,易证
,易证![]() .如图2,若点
.如图2,若点![]() 在直线l的异侧,其它条件不变,
在直线l的异侧,其它条件不变,![]() 是否依然成立?若成立,请写出证明过程;若不成立,请说明理由.
是否依然成立?若成立,请写出证明过程;若不成立,请说明理由.
(2)变式一:如图3,![]() 中,
中,![]() ,直线l经过点
,直线l经过点![]() ,点
,点![]() 、
、![]() 分别在直线l上,点
分别在直线l上,点![]() 、
、![]() 位于l的同一侧,如果
位于l的同一侧,如果![]() ,求证:
,求证:![]() .
.
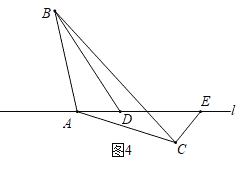
(3)变式二:如图4,![]() 中,依然有
中,依然有![]() ,若点
,若点![]() ,
,![]() 位于l的两侧,如果
位于l的两侧,如果![]() ,
,![]() ,求证:
,求证:![]() .
.
【答案】(1)成立,理由见解析(2)见解析(3)见解析
【解析】
(1)K型全等模型的基本型,通过在△ACE和△ADB中利用角的互余关系证明等角,从而证明全等;
(2)一线三角的基本型,通过△AEC和△ADB中内角和180°证明等角,从而证明全等;
(3)一线三角的变式,通过△ADB和△ACE中内角和与外角的关系证明等角,从而证明全等.
(1)成立,理由如下:
在Rt△ADB中,∠ABD+∠BAD=90°
在Rt△AEC中,∠CAE+∠ACE=90°
∵∠BAC=90°
∴∠BAD+∠EAC=90°
∴∠ABD=∠CAE
∵AB=AC
∴△AEC≌△ABD(AAS)
(2)在△ABD中,∠D+∠BAD+∠ABD=180°
在△BEC中,∠E+∠CEA+∠EAC=180°
∵∠CAE+∠CAB+∠BAD=180°
∴∠E=∠D,∠CAE=∠ABD
∴△ACE≌△ADB(AAS)
(3)如图4,设∠ABC=![]() ,∠BFD=
,∠BFD=![]()
∵∠BDA+∠BAC=180°,∠BDA=∠AEC
∴∠BDA=∠AEC=2![]()
∴∠DBF=2![]()
![]()
∴∠ABD=![]()
![]()
∴∠EAC=![]()
![]()
∴△ABD≌△CAE(AAS)
∴CE=AD,AE=BD
∵AE=AD+DE
∴BD=CE+DE

练习册系列答案
相关题目