题目内容
【题目】已知关于x的一元二次方程x2+2x+2k-5=0有两个实数根.
(1)求实数k的取值范围.
(2)若方程的一个实数根为4,求k的值和另一个实数根.
(3)若k为正整数,且该方程的根都是整数,求k的值.
【答案】(1)k≤3;(2)k的值为-![]() ,另一个根为-6;(3)k的值为1或3.
,另一个根为-6;(3)k的值为1或3.
【解析】
(1)根据一元二次方程根的判别式列不等式即可得答案;
(2)根据一元二次方程根与系数的关系即可得答案;
(3)由(1)可得k≤3,根据k为正整数可得k=1,k=2或k=3,分别代入方程,求出方程的根,根据该方程的根都是整数即可得答案.
(1)∵关于x的一元二次方程x2+2x+2k﹣5=0有两个实数根,
∴△=22﹣4×1×(2k﹣5)=﹣8k+24≥0,
解得:k≤3,
∴k的取值范围是k≤3.
(2)设方程的另一个根为m,
∴4+m=-2,
解得:m=-6,
∴2k﹣5=4×(-6)
∴k=-![]() ,
,
∴k的值为-![]() ,另一个根为-6.
,另一个根为-6.
(3)∵k为正整数,且k≤3,
∴k=1或k=2或k=3,
当k=1时,原方程为x2+2x﹣3=0,解得x1=﹣3,x2=1,
当k=2时,原方程为x2+2x-1=0,解得x1=-1+![]() ,x2=-1-
,x2=-1-![]() ,(舍去)
,(舍去)
当k=3时,原方程为x2+2x+1=0,解得x1=x2=-1,
∴k的值为1或3.

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
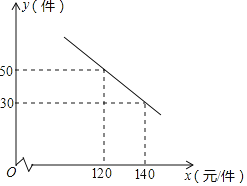
单元期中期末卷系列答案【题目】某文具店购进一批纪念册,每本进价为20元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间具有某种函数关系,其对应规律如下表所示
售价x(元/本) | … | 22 | 23 | 24 | 25 | 26 | 27 | … |
销售量y(件) | … | 36 | 34 | 32 | 30 | 28 | 26 | … |
(1)请直接写出y与x的函数关系式: .
(2)设该文店每周销售这种纪念册所获得的利润为W元,写出W与x之间的函数关系式,并求出该纪念册的销售单价定为多少元时,才能使文具店销售该纪念册每周所获利润最大?最大利润是多少?