题目内容
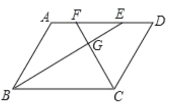
【题目】如图,在□ABCD中,∠ABC,∠BCD的平分线分别交AD于点E,F,BE,CF相交于点G.
(1)求证:BE⊥CF;
(2)若AB=a,CF=b,求BE的长.
【答案】(1)见详解;(2)![]() .
.
【解析】
(1)由平行四边形的性质和角平分线的性质,证明∠EBC+∠FCB=90°即可解决问题;
(2)如图,作EH∥AB交BC于点H,连接AH交BE于点P.构造特殊四边形菱形,利用菱形的性质,结合勾股定理即可解决问题;
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
∵BE,CF分别是∠ABC,∠BCD的平分线,
∴∠EBC=![]() ∠ABC,∠FCB=
∠ABC,∠FCB=![]() ∠BCD,
∠BCD,
∴∠EBC+∠FCB=90°,
∴∠BGC=90°.
即BE⊥CF.
(2)如图,作EH∥AB交BC于点H,连接AH交BE于点P.
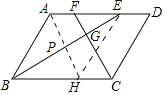
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵AD∥BC,
∴∠AEB=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
∴四边形ABHE是菱形,
∴AH,BE互相垂直平分;
∵BE⊥CF,
∴AH∥CF,
∴四边形AHCF是平行四边形,
∴AP=![]() ;
;
在Rt△ABP中,由勾股定理,得:
![]() ,
,
∴![]() .
.

练习册系列答案
相关题目