Question

【题目】如图，已知线段AB=2，点P是线段AB上一点，分别以AP、BP为边作两个正方形.

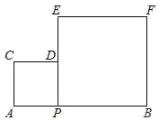
（1）如果APx，求两个正方形的面积之和S；

（2）当点P是AB的中点时，求两个正方形的面积之和S1；

（3）当点P不是AB的中点时，比较（1）中的S与（2）中S1的大小.

Answer 1

【答案】（1）；（2）；（3）.

【解析】

（1）根据正方形的面积公式，可得每个正方形的面积，根据整式的加减即可求解；

（2）根据正方形的面积公式，可得正方形的面积，根据有理数的加法即可求解；

（3）根据整式的加减进行化解，再根据完全平方公式的特点即可求解.

（1）APx，BP=2-x,

S=S正方形APCD+ S正方形PBFE

=x2+(2-x)2

=

（2）当点P是AB的中点时，AP1，BP=1,

∴S1= S正方形APCD+ S正方形PBFE

= AP2+BP2

=2

（3）当点P不是AB的中点时，得x≠1，

∴S- S1=-2==2()=2

∵x≠1，∴2＞0，

故.