题目内容
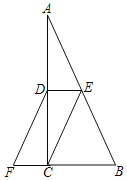
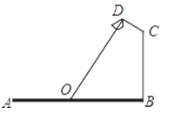
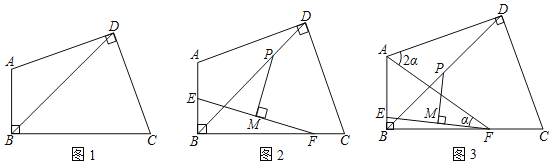
【题目】如图1，四边形ABCD中，∠ABC＝∠ADC＝90°，AD＝CD．
（1）求证：BD平分∠ABC；
（2）如图2，点E、F分别在AB、BC上，连接EF，M是EF的中点，过M作EF的垂线交BD于P．求证：AE+CF＝
PD；
（3）如图3，在（2）条件下，连AF，若AE＝CF，∠DAF＝2∠AFE＝2α，AF＝13，BC＝12，（BC＞AB）．求BD的长．
【答案】（1）见解析；（2）见解析；（3）17
【解析】
（1）作DG⊥BC于G，DH⊥BA于H，通过证明△DAH≌△DCG可证点D到BA和BC的距离相等；
（2）PM是中垂线，因此连接PE、PF，有PE＝PF，由第（1）问可知∠ABD＝∠CBD，则B、E、P、F四点共圆，推出∠EPF是直角，将△BEP绕点P逆时针旋转90°至△NFP，可以得出BE+BF＝
BP，注意四边形ABCD的结构与四边形PEBF结构一样，因此同理可得AB+BC＝BD，进而得出所证结论．
（3）由于AE＝CF，因此可以考虑CF为边在BC上方构造△QCF≌△FEA，连接AQ、AC．可以推出△AFQ是等腰直角三角形，同时注意△ACD也是等腰直角三角形，∠CAQ是两个45°的重叠角，于是∠CAQ＝90﹣2α，然后可推出AC＝AQ，而AQ＝AF＝13，BC已知，由勾股定理可算出AB长度，根据第（2）问中的结论，BD长度就自然得出．
解：（1）如图1，作DG⊥BC于G，DH⊥BA于H．
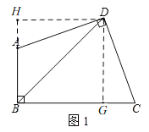
则∠DHA＝∠DGC＝90°．
∵∠ABC＝∠ADC＝90°，
∴∠BAD+∠BCD＝180°，
∵∠BAD+∠DAH＝180°，
∴∠DAH＝∠DCG，
在△DAH和△DCG中：
，
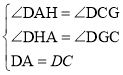∴△DAH≌△DCG（AAS），
∴DH＝DG，
∴BD平分∠ABC．
（2）如图2，连接PE、PF，
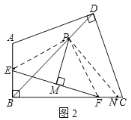
∵M为EF中点且PM⊥EF，
∴PE＝PF，
∵∠EBP＝∠FBP，
∴P、E、B、F四点共圆，
∴∠PEB+∠PFB＝∠EBF+∠EPF＝180°，
∴∠EBF＝90°，
∴∠EPF＝90°，
在FC上截取FN＝BE，连接PN．
∴∠PFN+∠PFB＝180°，
∴∠PFN＝∠PEB，
在△PEB和△PFN中：
，
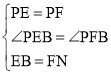∴△PEB≌△PFN（SAS），
∴PB＝PN，∠EPB＝∠FPN
∴∠BPN＝∠BPF+∠FPN＝∠BPF+∠EPB＝∠EPF＝90°，
∴△BPN是等腰直角三角形，
∴BN＝BP，
∵BN＝BF+FN＝BF+BE，
∴BE+BF＝BP，
同理可证BA+BC＝BD，
∴AE+BE+BF+FC＝(BP+PD)＝BP+PD，
∴AE+CF＝PD．
（3）如图3，作△QCF≌△FEA，连接AQ、AC．
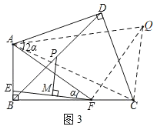
则∠EAF＝∠CFQ，AF＝FQ，∠FQC＝∠AFE＝α，
∵∠EAF+∠AFB＝90°，
∴∠CFQ+∠AFB＝90°，
∴∠AFQ＝90°，
∴△AFQ是等腰直角三角形，
∴AQ＝AF＝13，∠FAQ＝∠FQA＝45°，
∵AD＝DC，∠ADC＝90°，
∴△ADC是等腰直角三角形，
∴∠DAC＝∠DCA＝45°，
∴∠DAC+∠FAQ＝∠DAF+∠QAC＝90°，
∴∠QAC＝90°﹣∠DAC＝90°﹣2α，
∵∠AQC＝∠AQF+∠FQC＝45°+α，
∴∠ACQ＝180°﹣∠QAC﹣∠AQC＝45°+α，
∴AC＝AQ＝13，
∵BC＝12，
∴AB＝5，
由（2）可知AB+BC＝BD，
∴BD＝
(AB+BC)＝17．
