ЬтФПФкШн
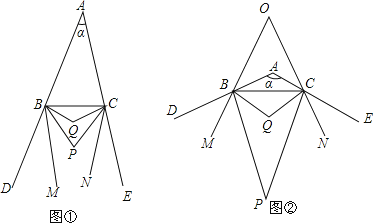
ЁОЬтФПЁПвбжЊШчЭМЂйЃЌBPЁЂCPЗжБ№ЪЧЁїABCЕФЭтНЧЁЯCBDЁЂЁЯBCEЕФНЧЦНЗжЯпЃЌBQЁЂCQЗжБ№ЪЧЁЯPBCЁЂЁЯPCBЕФНЧЦНЗжЯпЃЌBMЁЂCNЗжБ№ЪЧЁЯPBDЁЂЁЯPCEЕФНЧЦНЗжЯпЃЌЁЯBACЃНІСЃЎ
ЃЈ1ЃЉЕБІСЃН40ЁуЪБЃЌЁЯBPCЃНЁЁ ЁЁЁуЃЌЁЯBQCЃНЁЁ ЁЁЁуЃЛ
ЃЈ2ЃЉЕБІСЃНЁЁ ЁЁЁуЪБЃЌBMЁЮCNЃЛ
ЃЈ3ЃЉШчЭМЂкЃЌЕБІСЃН120ЁуЪБЃЌBMЁЂCNЫљдкжБЯпНЛгкЕуOЃЌЧѓЁЯBOCЕФЖШЪ§ЃЛ
ЃЈ4ЃЉдкІСЃО60ЁуЕФЬѕМўЯТЃЌжБНгаДГіЁЯBPCЁЂЁЯBQCЁЂЁЯBOCШ§НЧжЎМфЕФЪ§СПЙиЯЕЃКЁЁ ЁЁЃЎ
ЁОД№АИЁПЃЈ1ЃЉ70ЃЌ 125ЃЛЃЈ2ЃЉ60ЃЛЃЈ3ЃЉ45ЁуЃЛЃЈ4ЃЉЁЯBPC+ЁЯBQC+ЁЯBOCЃН180ЁуЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнШ§НЧаЮЕФЭтНЧаджЪЗжБ№БэЪОГіЁЯDBCгыЁЯBCEЃЌдйИљОнНЧЦНЗжЯпЕФаджЪПЩЧѓЕУЁЯCBP+ЁЯBCPЃЌзюКѓИљОнШ§НЧаЮФкНЧКЭЖЈРэМДПЩЧѓНтЃЛИљОнНЧЦНЗжЯпЕФЖЈвхЕУГіЁЯQBCЃН![]() ЁЯPBCЃЌЁЯQCBЃН
ЁЯPBCЃЌЁЯQCBЃН![]() ЁЯPCBЃЌЧѓГіЁЯQBC+ЁЯQCBЕФЖШЪ§ЃЌИљОнШ§НЧаЮФкНЧКЭЖЈРэЧѓГіМДПЩЃЛ
ЁЯPCBЃЌЧѓГіЁЯQBC+ЁЯQCBЕФЖШЪ§ЃЌИљОнШ§НЧаЮФкНЧКЭЖЈРэЧѓГіМДПЩЃЛ
ЃЈ2ЃЉИљОнЦНааЯпЕФаджЪЕУЕНЁЯMBC+ЁЯNCBЃН180ЁуЃЌвРДЫЧѓНтМДПЩЃЛ
ЃЈ3ЃЉИљОнЬтвтЕУЕНЁЯMBC+ЁЯNCBЃЌдйИљОнШ§НЧаЮЭтНЧЕФаджЪКЭШ§НЧаЮФкНЧКЭЖЈРэЕУЕНЁЯBOCЕФЖШЪ§ЃЛ
ЃЈ4ЃЉЗжБ№гУЁЯAБэЪОГіЁЯBPCЁЂЁЯBQCЁЂЁЯBOCЃЌдйЯрМгМДПЩЧѓНтЃЎ
НтЃКЃЈ1ЃЉЁпЁЯDBCЃНЁЯA+ЁЯACBЃЌЁЯBCEЃНЁЯA+ЁЯABCЃЌ
ЁрЁЯDBC+ЁЯBCEЃН180Ёу+ЁЯAЃН220ЁуЃЌ
ЁпBPЁЂCPЗжБ№ЪЧЁїABCЕФЭтНЧЁЯCBDЁЂЁЯBCEЕФНЧЦНЗжЯпЃЌ
ЁрЁЯCBP+ЁЯBCPЃН![]() ЃЈЁЯDBC+ЁЯBCEЃЉЃН110ЁуЃЌ
ЃЈЁЯDBC+ЁЯBCEЃЉЃН110ЁуЃЌ
ЁрЁЯBPCЃН180ЁуЉ110ЁуЃН70ЁуЃЌ
ЁпBQЁЂCQЗжБ№ЪЧЁЯPBCЁЂЁЯPCBЕФНЧЦНЗжЯпЃЌ
ЁрЁЯQBCЃН![]() ЁЯPBCЃЌЁЯQCBЃН
ЁЯPBCЃЌЁЯQCBЃН![]() ЁЯPCBЃЌ
ЁЯPCBЃЌ
ЁрЁЯQBC+ЁЯQCBЃН55ЁуЃЌ
ЁрЁЯBQCЃН180ЁуЉ55ЁуЃН125ЁуЃЛ
ЃЈ2ЃЉЁпBMЁЮCNЃЌ
ЁрЁЯMBC+ЁЯNCBЃН180ЁуЃЌ
ЁпBMЁЂCNЗжБ№ЪЧЁЯPBDЁЂЁЯPCEЕФНЧЦНЗжЯпЃЌЁЯBACЃНІСЃЌ
Ёр![]() ЃЈЁЯDBC+ЁЯBCEЃЉЃН180ЁуЃЌ
ЃЈЁЯDBC+ЁЯBCEЃЉЃН180ЁуЃЌ
МД![]() ЃЈ180Ёу+ІСЃЉЃН180ЁуЃЌ
ЃЈ180Ёу+ІСЃЉЃН180ЁуЃЌ
НтЕУІСЃН60ЁуЃЛ
ЃЈ3ЃЉЁпІСЃН120ЁуЃЌ
ЁрЁЯMBC+ЁЯNCBЃН![]() ЃЈЁЯDBC+ЁЯBCEЃЉЃН
ЃЈЁЯDBC+ЁЯBCEЃЉЃН![]() ЃЈ180Ёу+ІСЃЉЃН225ЁуЃЌ
ЃЈ180Ёу+ІСЃЉЃН225ЁуЃЌ
ЁрЁЯBOCЃН225ЁуЉ180ЁуЃН45ЁуЃЛ
ЃЈ4ЃЉЁпІСЃО60ЁуЃЌ
ЁЯBPCЃН90ЁуЉ![]() ІС
ІС
ЁЯBQCЃН135ЁуЉ![]() ІС
ІС
ЁЯBOCЃН![]() ІСЉ45ЁуЃЎ
ІСЉ45ЁуЃЎ
ЁЯBPCЁЂЁЯBQCЁЂЁЯBOCШ§НЧжЎМфЕФЪ§СПЙиЯЕЃКЁЯBPC+ЁЯBQC+ЁЯBOCЃНЃЈ90ЁуЉ![]() ІСЃЉ+ЃЈ135ЁуЉ
ІСЃЉ+ЃЈ135ЁуЉ![]() ІСЃЉ+ЃЈ
ІСЃЉ+ЃЈ![]() ІСЉ45ЁуЃЉЃН180ЁуЃЎ
ІСЉ45ЁуЃЉЃН180ЁуЃЎ
ЙЪД№АИЮЊЃК70ЃЌ125ЃЛ60ЃЛЁЯBPC+ЁЯBQC+ЁЯBOCЃН180ЁуЃЎ



