题目内容
【题目】问题探究
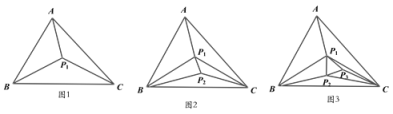
(1)如图1,△ABC和△DEC均为等腰直角三角形,且∠BAC=∠CDE=90°,AB=AC=3,DE=CD=1,连接AD、BE,求![]() 的值;
的值;
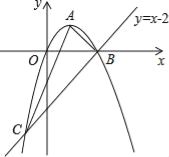
(2)如图2,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=4,过点A作AM⊥AB,点P是射线AM上一动点,连接CP,做CQ⊥CP交线段AB于点Q,连接PQ,求PQ的最小值;

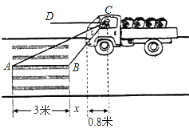
(3)李师傅准备加工一个四边形零件,如图3,这个零件的示意图为四边形ABCD,要求BC=4cm,∠BAD=135°,∠ADC=90°,AD=CD,请你帮李师傅求出这个零件的对角线BD的最大值。
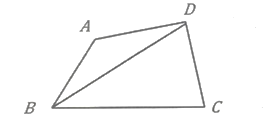
图3
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() +
+![]() .
.
【解析】
(1)由等腰直角三角形的性质可得BC=3![]() ,CE=
,CE=![]() ,∠ACB=∠DCE=45°,可证△ACD∽△BCE,可得
,∠ACB=∠DCE=45°,可证△ACD∽△BCE,可得![]() =
=![]() ;
;
(2)由题意可证点A,点Q,点C,点P四点共圆,可得∠QAC=∠QPC,可证△ABC∽△PQC,可得![]() ,可得当QC⊥AB时,PQ的值最小,即可求PQ的最小值;
,可得当QC⊥AB时,PQ的值最小,即可求PQ的最小值;
(3)作∠DCE=∠ACB,交射线DA于点E,取CE中点F,连接AC,BE,DF,BF,由题意可证△ABC∽△DEC,可得![]() ,且∠BCE=∠ACD,可证△BCE∽△ACD,可得∠BEC=∠ADC=90°,由勾股定理可求CE,DF,BF的长,由三角形三边关系可求BD的最大值.
,且∠BCE=∠ACD,可证△BCE∽△ACD,可得∠BEC=∠ADC=90°,由勾股定理可求CE,DF,BF的长,由三角形三边关系可求BD的最大值.
(1)∵∠BAC=∠CDE=90°,AB=AC=3,DE=CD=1,
∴BC=3![]() ,CE=
,CE=![]() ,∠ACB=∠DCE=45°,
,∠ACB=∠DCE=45°,
∴∠BCE=∠ACD,
∵![]() =
=![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() =
=![]() ,∠BCE=∠ACD,
,∠BCE=∠ACD,
∴△ACD∽△BCE,
∴![]() =
=![]() ;
;
(2)∵∠ACB=90°,∠B=30°,BC=4,
∴AC=![]() ,AB=2AC=
,AB=2AC=![]() ,
,
∵∠QAP=∠QCP=90°,
∴点A,点Q,点C,点P四点共圆,
∴∠QAC=∠QPC,且∠ACB=∠QCP=90°,
∴△ABC∽△PQC,
∴![]() ,
,
∴PQ=![]() ×QC=
×QC=![]() QC,
QC,
∴当QC的长度最小时,PQ的长度最小,
即当QC⊥AB时,PQ的值最小,
此时QC=2,PQ的最小值为![]() ;
;
(3)如图,作∠DCE=∠ACB,交射线DA于点E,取CE中点F,连接AC,BE,DF,BF,
 ,
,
∵∠ADC=90°,AD=CD,
∴∠CAD=45°,∠BAC=∠BAD-∠CAD=90°,
∴△ABC∽△DEC,
∴![]() ,
,
∵∠DCE=∠ACB,
∴∠BCE=∠ACD,
∴△BCE∽△ACD,
∴∠BEC=∠ADC=90°,
∴CE=![]() BC=2
BC=2![]() ,
,
∵点F是EC中点,
∴DF=EF=![]() CE=
CE=![]() ,
,
∴BF=![]() =
=![]() ,
,
∴BD≤DF+BF=![]() +
+![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】(问题背景)在△ABC内部,有地点![]() ,可构成3个不重叠的小三角形(如图1)
,可构成3个不重叠的小三角形(如图1)
(探究发现)当△ABC内的点的个数增加时,若其他条件不变,探究三角形内互不重叠的小三角形的个数情况。
(1)填表:
三角形内点的个数n | 1 | 2 | 3 | 4 | …… |
不重叠三角形个数S | …… |
(2)当△ABC内部有2019个点(![]() ,
,![]() ……
……![]() )时,三角形内不重叠的小三角形的个数S为多少?
)时,三角形内不重叠的小三角形的个数S为多少?