Question

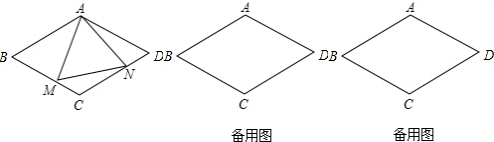
如图，以等边△OAB的高OC为边向逆时针方向作等边△OCD，CD交OB于点E，再以OE为边向逆时针方向作等边△OEF，EF交OD于点G，再以OG为边向逆时针方向作等边△OGH，…，按此方法操作，最后得到△OMN，此时N在AO延长线上．若AB=1，则ON=______．

Answer 1

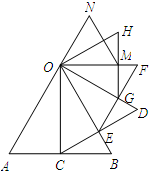
∵等边△ABC的边长为1，OC⊥AB，
∴OC=OA•sin60°=1×

3

2

=

3

2

，
同理，OE=OC•sin60°=

3

2

×

3

2

=（

3

2

）²=

3

4

，
OG=OE•sin60°=

3

4

×

3

2

=（

3

2

）³=

3 3

8

，
故OM=ON=（

3

2

）⁴=

9

16

．
故答案为：

9

16

．