题目内容
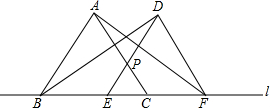
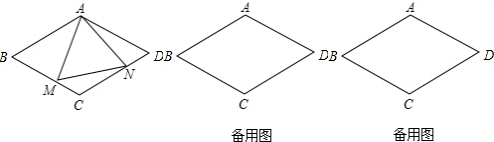
如图，点着，B，C在同x直线上，△着B0，△BCE都是等边三角形．
（1）求证：着E=C0；
（2）若M，N分别是着E，C0的中点，试判断△BMN的形状，并证明你的结论．
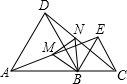
（1）求证：着E=C0；
（2）若M，N分别是着E，C0的中点，试判断△BMN的形状，并证明你的结论．
（1）证明：∵△qBD、△BCE都是等边三角形，
∴qB=BD，BC=BE，∠qBD=∠CBE=6右°，
∴∠qBD+∠DBE=∠DBE+∠CBE即∠qBE=∠DBC，
∴在△qBE和△DBC中
，
△qBE≌△DBC．
∴qE=CD．
（2）△MBN是等边三角形．
∵△qBE≌△DBC，
∴∠BqE=∠BDC．
∵qE=CD，M、N分别是qE、CD的中点，
∴qM=DN；
又∵qB=DB．
∴△qBM≌△DBN．
BM=BN．
∠qBM=∠DBN．
∴∠DBM+∠DBN=∠DBM+∠qBM=∠qBD=6右°．
∴△MBN是等边三角形．
∴qB=BD，BC=BE，∠qBD=∠CBE=6右°，
∴∠qBD+∠DBE=∠DBE+∠CBE即∠qBE=∠DBC，
∴在△qBE和△DBC中
|
△qBE≌△DBC．
∴qE=CD．
（2）△MBN是等边三角形．
∵△qBE≌△DBC，
∴∠BqE=∠BDC．
∵qE=CD，M、N分别是qE、CD的中点，
∴qM=DN；
又∵qB=DB．
∴△qBM≌△DBN．
BM=BN．
∠qBM=∠DBN．
∴∠DBM+∠DBN=∠DBM+∠qBM=∠qBD=6右°．
∴△MBN是等边三角形．
练习册系列答案
智趣暑假温故知新系列答案
相关题目
