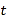题目内容
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式;
(2)求出四边形ABPC的面积最大时的P点坐标和四边形ABPC的最大面积;
(3)在直线BC找一点Q,使得△QOC为等腰三角形,写出Q点坐标.

【答案】(1)y=x2﹣2x﹣3;(2)P点的坐标为(![]() ,﹣
,﹣![]() ),四边形ABPC的面积的最大值为
),四边形ABPC的面积的最大值为![]() ;(3)Q点坐标为(
;(3)Q点坐标为(![]() ,
,![]() ﹣3)、(﹣
﹣3)、(﹣![]() ,﹣
,﹣![]() ﹣3)、(3,0)或(
﹣3)、(3,0)或(![]() ,﹣
,﹣![]() ).
).
【解析】
(1)把B、C两点的坐标代入二次函数y=x2+bx+c即可求出b,c的值,故可得出二次函数的解析式;
(2)过点P作y轴的平行线与BC交于点Q,与OB交于点E,设P(x,x2﹣2x﹣3),易得,直线BC的解析式为y=x﹣3,则Q点的坐标为(x,x﹣3),再根据S四边形ABPC=S△ABC+S△BPQ+S△CPQ即可得出结论;
(3)分当OC=QC时,当OC=QO时,当QC=QO时三种情况求解即可.
解:(1)将B、C两点的坐标代入得![]() ,
,
解得:![]() ;
;
所以二次函数的表达式为:y=x2﹣2x﹣3;
(2)如图,过点P作y轴的平行线与BC交于点Q,与OB交于点F,
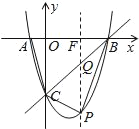
设P(x,x2﹣2x﹣3),设直线BC的解析式为:y=kx+d,
则![]() ,
,
解得:![]() ,
,
∴直线BC的解析式为y=x﹣3,
则Q点的坐标为(x,x﹣3);
由0=x2﹣2x﹣3,解得:x1=﹣1,x2=3,
∴AO=1,AB=4,
S四边形ABPC=S△ABC+S△BPQ+S△CPQ
=![]() ABOC+
ABOC+![]() QPBF+
QPBF+![]() QPOF
QPOF
=![]() ×4×3+
×4×3+![]() (﹣x2+3x)×3
(﹣x2+3x)×3
=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() .
.
当x=![]() 时,四边形ABPC的面积最大
时,四边形ABPC的面积最大
此时P点的坐标为(![]() ,﹣
,﹣![]() ),四边形ABPC的面积的最大值为
),四边形ABPC的面积的最大值为![]() ;
;
(3)设点Q的坐标为(m,m﹣3),
∵O(0,0),C(0,﹣3),
∴OC=3,QC=![]() =
=![]() |m|,QO=
|m|,QO=![]() .
.
△QOC为等腰三角形分三种情况:
①当OC=QC时,3=![]() |m|,
|m|,
解得:m=±![]() ,
,
此时点Q的坐标为(![]() ,
,![]() ﹣3)或(﹣
﹣3)或(﹣![]() ,﹣
,﹣![]() ﹣3);
﹣3);
②当OC=QO时,3=![]() ,
,
解得:m=3或m=0(舍去),
此时点Q的坐标为(3,0);
③当QC=QO时,有![]() |m|=
|m|=![]() ,
,
解得:m=![]() ,
,
此时点Q的坐标为(![]() ,﹣
,﹣![]() ).
).
综上可知:Q点坐标为(![]() ,
,![]() ﹣3)、(﹣
﹣3)、(﹣![]() ,﹣
,﹣![]() ﹣3)、(3,0)或(
﹣3)、(3,0)或(![]() ,﹣
,﹣![]() ).
).

 名校课堂系列答案
名校课堂系列答案【题目】甲、乙两名队员参加设计训练,成绩分别被制成下列两个统计图:
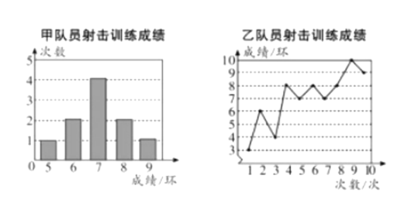
根据以上信息,整理分析数据如下:
平均数(环) | 中位数(环) | 众数(环) | 方差 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
(1)表格中![]() ,
,![]() ,
,![]() ;
;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩,若选派其中一名参赛,你认为应选哪名队员?
(3)如果乙再射击![]() 次,命中
次,命中![]() 环,那么乙的射击成绩的方差 .(填“变大”“变小”或“不变”)
环,那么乙的射击成绩的方差 .(填“变大”“变小”或“不变”)