题目内容
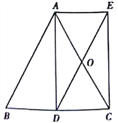
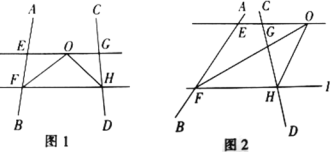
【题目】[探究]如图,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB,CD交于点E、G.
(1)若∠AFH=60°,∠CHF=50°,则∠EOF= °,∠ FOH= °
(2)若∠AFH+∠CHF= 100°,求∠FOH的度数.
(3)当∠FOH=_____ °时 ,AB//CD.
[拓展]如图,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB,CD交于点E、G.若∠AFH+∠CHF=a,求∠FOH的度数. (用含a的代数式表示)
【答案】(1)30,125;(2) 130°;(3)90°;拓展: 90°-![]() a.
a.
【解析】
(1)依据角平分线以及平行线的性质,即可得到∠EOF的度数,依据三角形内角和定理,即可得到∠FOH的度数;(2)依据角平分线以及平行线的性质、三角形内角和定理,即可得到∠FOH的度数; (3) 因为∠OFH=![]() ∠AFH,∠OHF=
∠AFH,∠OHF=![]() ∠CHF,所以∠OFH+∠CHF=
∠CHF,所以∠OFH+∠CHF=![]() (∠AFH+∠CHF),当∠AFH+∠CHF=180°时,AB//CD,此时 ∠OFH+∠CHF=
(∠AFH+∠CHF),当∠AFH+∠CHF=180°时,AB//CD,此时 ∠OFH+∠CHF=![]() (∠AFH+∠CHF)=
(∠AFH+∠CHF)=![]() ×180°=90° ,根据三角形内角和得:∠FOH=180°-(∠OFH+∠CHF )=90°.
×180°=90° ,根据三角形内角和得:∠FOH=180°-(∠OFH+∠CHF )=90°.
【拓展】根据∠AFH和∠CHI的平分线交于点O,可得∠OFH=![]() ∠AFH,∠OHI=
∠AFH,∠OHI=![]() ∠CHI,再根据∠FOH=∠OHI-∠OFH进行计算,即可得到∠FOH的度数.
∠CHI,再根据∠FOH=∠OHI-∠OFH进行计算,即可得到∠FOH的度数.
解,【探究】(1) )∵∠AFH=60°,OF平分∠AFH,
∴∠OFH=30°,
又∵EG∥FH,
∴∠EOF=∠OFH=30°;
∵∠CHF=50°,OH平分∠CHF,
∴∠FHO=25°,
∴△FOH中,∠FOH=180°-∠OFH-∠OHF=125°;
故答案为:30,125.
(2)因为FO平分∠AFH,HO平分∠CHF. 所以∠OFH=![]() ∠AFH,∠OHF=
∠AFH,∠OHF=![]() ∠CHF.
∠CHF.
因为∠AFH+∠CHF=100°,所以∠OFH+∠OHF=![]() (∠AFH+∠CHF)=50°
(∠AFH+∠CHF)=50°
∵EG∥FH,
∴∠EOF=∠OFH,∠GOH=∠OHF.
∴∠EOF+∠GOH=∠OFH+∠OHF=50°.
∵∠EOF+∠GOH+∠FOH=180°,
所以∠FOH= 180°-(∠OFH+∠OHF)=180°-50°![]() =130°.
=130°.
(3) ∵∠OFH=![]() ∠AFH,∠OHF=
∠AFH,∠OHF=![]() ∠CHF,
∠CHF,
∴∠OFH+∠CHF=![]() (∠AFH+∠CHF),
(∠AFH+∠CHF),
当∠AFH+∠CHF=180°时,AB//CD,此时 ∠OFH+∠CHF=![]() (∠AFH+∠CHF)=
(∠AFH+∠CHF)=![]() ×180°=90° ,根据三角形内角和得:∠FOH=180°-(∠OFH+∠CHF )=90°.
×180°=90° ,根据三角形内角和得:∠FOH=180°-(∠OFH+∠CHF )=90°.
【拓展】
因为∠AFH和∠CHI的平分线交干点O.
所以∠OFH=![]() ∠AFH,∠OHI=
∠AFH,∠OHI=![]() ∠CHI.
∠CHI.
因为EG//FH,所以∠EOH=∠OHI,∠EOF=∠OFH.
因为∠FOH=∠EOH-∠EOF,∠FOH=∠OHI-∠EOH=![]() (∠CHI-∠AFH)=90°-
(∠CHI-∠AFH)=90°-![]() a.
a.