题目内容
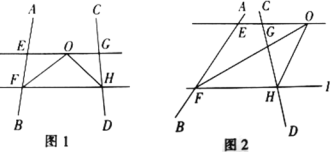
【题目】如图,河的两岸l1与l2相互平行,A,B是l1上的两点,C,D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
【答案】解:过点D作l1的垂线,垂足为F,

∵∠DEB=60°,∠DAB=30°,
∴∠ADE=∠DEB﹣∠DAB=30°,
∴△ADE为等腰三角形,
∴DE=AE=20,
在Rt△DEF中,EF=DEcos60°=20× ![]() =10,
=10,
∵DF⊥AF,
∴∠DFB=90°,
∴AC∥DF,
由已知l1∥l2,
∴CD∥AF,
∴四边形ACDF为矩形,CD=AF=AE+EF=30,
答:C、D两点间的距离为30m.
【解析】解直角三角形须把特殊角放到直角三角形中,因此须过点D作l1的垂线,构造直角三角形,由已知得△ADE为等腰三角形,得出DE=AE=20,在Rt△DEF中,EF=DEcos60°=20× 1 2 =10,进而算出C、D两点间的距离为30m.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目