题目内容
【题目】如图，AB∥CD，则∠A、∠C、∠E、∠F满足的数量关系是（ ）
A.∠A＝∠C＋∠E＋∠FB.∠A＋∠E－∠C－∠F＝180°
C.∠A＋∠C－∠E－∠F＝180°D.∠A＋∠E＋∠C＋∠F＝360°
【答案】C
【解析】
过点A作MN∥FC，MN交EF于G点，延长BA交EF于点H，根据题意利用平行线性质以及三角形外角性质得出∠C=∠1，∠2+∠1=180°，∠4=∠E+∠3，∠2=∠EAB∠4，由此进一步分析求解即可.
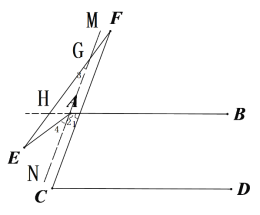
如图，过点A作MN∥FC，延长BA交EF于点H，
∵AB∥CD，
∴∠C=∠1，
∵MN∥FC，
∴∠2+∠1=180°，∠3=∠F，
∵∠4=∠E+∠3，∠2=∠EAB∠4，
∴∠1+∠EAB∠4＝180°
即：∠A+∠C－∠E－∠F=180°，
故选：C.
练习册系列答案
相关题目
【题目】抛物线
上部分点的横坐标x，纵坐标y的对应值如下表：
x |
|
|
| 0 | 1 | 2 |
|
y |
| 0 | 4 | 6 | 6 | 4 |
|
小聪观察上表，得出下面结论：
抛物线与x轴的一个交点为
；
函数的最大值为6；
抛物线的对称轴是
；
在对称轴左侧，y随x增大而增大
其中正确有
A. 
B. 
C. 
D. 
