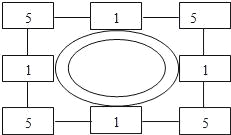
题目内容
【题目】观察下边各式,你发现什么规律:将你猜想到的规律用只含有一个字母的等式表示出来__________.

【答案】(2n-1)(2n+1)=(2n)2-1.
【解析】
利用(2×1-1)(2×1+1)=(2×1)2-1;(2×2-1)×(2×2+1)=(2×2)2-1;(2×3-1)×(2×3+1)=(2×3)2-1,则可以得出第n个等式为(2n-1)(2n+1)=(2n)2-1.
∵(2×1-1)(2×1+1)=(2×1)2-1;
(2×2-1)×(2×2+1)=(2×2)2-1;
(2×3-1)×(2×3+1)=(2×3)2-1;
∴第n个等式为(2n-1)(2n+1)=(2n)2-1.
故答案为:(2n-1)(2n+1)=(2n)2-1.

练习册系列答案
相关题目