题目内容
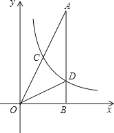
【题目】如图,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函数y=![]() 在第一象限内的图象分别交OA,AB于点C和点D,连结OD,△BOD的面积是4.
在第一象限内的图象分别交OA,AB于点C和点D,连结OD,△BOD的面积是4.
(1)求反比例函数解析式;
(2)将△AOB沿x轴向左运动,运动速度是每秒钟3个单位长度,求△AOB与反比例函数图象没有交点时,运动时间t的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据反比例函数系数k的几何意义即可确定反比例函数解析式;
(2)先求出A点恰好移到反比例函数图象上时点A的坐标,然后可得点A移动的距离和时间,进而可作判断.
解:(1)∵反比例函数y=![]() 在第一象限内,
在第一象限内,
∴k>0,
∵S△BOD=![]() k,
k,
∴![]() k=4,
k=4,
解得k=8,
∴反比例函数解析式为![]() ;
;
(2)当A点恰好移到![]() 上时,
上时,
∵AB=8,即为点A的纵坐标的值,
∴点A的横坐标是:![]() ,
,
∵OB=4,
∴点A移动的距离是4-1=3,移动的时间是3÷3=1秒,
所以若△AOB与反比例函数图象没有交点,则![]() .
.

练习册系列答案
相关题目