Question

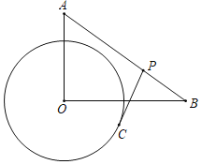
【题目】如图，在Rt△AOB中，∠AOB＝90°，OA＝3，OB＝4，⊙O的半径为2，点P是AB边上的动点，过点P作⊙O的一条切线PC（点C为切点），则线段PC长的最小值为_____．

Answer 1

【答案】

【解析】

连接OP，OC，由PC为圆O的切线，利用切线的性质得到OC与PC垂直，利用勾股定理列出关系式，由OP最小时，PC最短，根据垂线段最短得到OP垂直于AB时最短，利用面积法求出此时OP的值，再利用勾股定理即可求出PC的最短值．

连接OP、OC，如图所示，

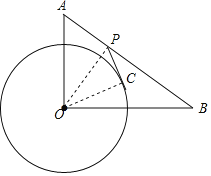
∵PC是⊙O的切线，

∴OC⊥PC，

根据勾股定理知：PC2＝OP2﹣OC2，

∴当PO⊥AB时，线段PC最短，

∵在Rt△AOB中，OA＝3，OB＝4，

∴AB＝5，

∴∴S△AOB＝OAOB＝ABOP，即OP＝＝，

∵OC＝2，

∴PC＝＝＝，

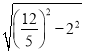故答案为：．