äãá¢áÖàï
àÓë¥È˜åÖƒÄÅöOABCøÅȘçÐAÀÂCçáæ½ÝõñøÝÞòúÈ´aȘ0ÈˋȘȴ0Ș
ÈˋȘçÐDòúüÔÑöBCèüçáÑ₤çÐÈ´ÆŠBÀÂCý£øĤüÈˋȘ¿»çÐDæ¼øÝüÔlȤy=-
x+b§£üÔÑöOAÆÖçÐEÈÛ
È´1ÈˋøݧÆÅÇ°—ƒÄÅöOABCçáûÌ£»È´Æû¤˜açáǺò»ò§ÝÚòƒÈˋÈ£
È´2ÈˋØîøˆa=3ȘçÝøÝüÔl§¨ƒÄÅöOABCñø°èøÉ°ÊüÁçàçáê§ý¢ñøòÝ
ÂìúµbçáøçÈ£
ÂÖäïÅöABDEçááÖý¢ÆÅØ£çÐPȘçÝÀîPÆŠABÀÂAEÀÂEDÑ¥üÁúÅòÝȘúµÀîPçᯊƒÑÈÛ
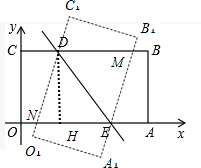
È´3ÈˋØîøˆa=5ȘඃÄÅöOABC¿ÄÆÖøÝüÔDEçáÑå°óë¥ÅööˆùáÝÔÅöO1A1B1C1ȘèÒCD=kȘçÝkôºæÐòýûÇä¾¥±òÝȘò¿ƒÄÅöOABC¤ëùáÝÔÅöO1A1B1C1çáøÄç±ý¢ñøçáûÌ£»öˆÑ´øçȘýÂúµ°—¡ûÑ´øçÈÛ
| 3 |
| 3 |
È´1ÈˋøݧÆÅÇ°—ƒÄÅöOABCçáûÌ£»È´Æû¤˜açáǺò»ò§ÝÚòƒÈˋÈ£
È´2ÈˋØîøˆa=3ȘçÝøÝüÔl§¨ƒÄÅöOABCñø°èøÉ°ÊüÁçàçáê§ý¢ñøòÝ
ÂìúµbçáøçÈ£
ÂÖäïÅöABDEçááÖý¢ÆÅØ£çÐPȘçÝÀîPÆŠABÀÂAEÀÂEDÑ¥üÁúÅòÝȘúµÀîPçᯊƒÑÈÛ
È´3ÈˋØîøˆa=5ȘඃÄÅöOABC¿ÄÆÖøÝüÔDEçáÑå°óë¥ÅööˆùáÝÔÅöO1A1B1C1ȘèÒCD=kȘçÝkôºæÐòýûÇä¾¥±òÝȘò¿ƒÄÅöOABC¤ëùáÝÔÅöO1A1B1C1çáøÄç±ý¢ñøçáûÌ£»öˆÑ´øçȘýÂúµ°—¡ûÑ´øçÈÛ

È´1ÈˋÀÔAÀÂCçáæ½ÝõñøÝÞòúÈ´aȘ0ÈˋȘȴ0Ș
ÈˋȘ
ÀÁOA=
ȘOA=aȘ
å·ƒÄÅöOABCçáûÌ£»òú
aȣ
È´2ÈˋÂìøÝüÔl§¨ƒÄÅöOABCñø°èøÉ°ÊüÁçàçáê§ý¢ñøȘ
ÀÁCD+OE=DB+EAȘ
DÈ´
Ș
ÈˋȘEÈ´
Ș0ÈˋȘ
ÀÁ
=6-
Șb=2
È£
ÂÖDÈ´1Ș
ÈˋÀÂEÈ´2Ș0ÈˋȘ
꘧ÆBEȘ
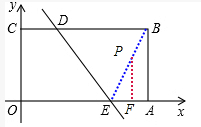
tanÀüBEA=tanÀüDEO=
Ș
DEO=60ÀÐ
ÀÁÀüBEA=ÀüBEDȘ
ÀÔÀîPÆŠABÀÂAEÀÂEDÑ¥üÁúÅȘ
ÀÁåýÅáPÝÄåÖBEèüȘ
¿»Pæ¼PFÀëOAȘǿæÐöˆFȘ
ÀÁÀ¼EPFÀæÀ¼EBAȘ
ÀÁ
=
Ș
èÒÀîPçᯊƒÑöˆrȘ
=
Ș
ÀÁr=
È£
È´3ÈˋÆèäãØãøˆÈ˜DMÀöNEȘDNÀöMEȘ
ÀÁùáÝÔÅöDNEMöˆó§ÅÅùáÝÔÅöȘ
¡ªƒïøÃÑå°óøˆÈ˜ÀüMED=ÀüNEDȘ
ÆøÀüMDE=ÀüNEDȘ
ÀÁÀüMED=ÀüMDEȘ
ÀÁMD=MEȘ
ÀÁó§ÅÅùáÝÔÅöDNEMöˆêãÅöÈÛ
çÝNÆŠOøĤüòÝȘCD=1Ș
çÝMÆŠBøĤüòÝȘCD=3Ș
ÀÁçÝ1ÀÉkÀÉ3òÝøÄç±ý¢ñøçáûÌ£»öˆÑ´øçÈÛ
¿»çÐDæ¼DHÀëOAȘǿæÐöˆHȘ
ÆèäãØãøˆÈ˜tanÀüDEN=
ȘDH=
Ș
ÀÁHE=1Ș
èÒêãÅöDNEMçáÝÔ°ÊöˆaȘ
å·åÖRtÀ¼DHNøÅȘÆè¿Ç¿èÑ´âÚøˆÈ˜
a2=È´a-1Èˋ2+È´
Èˋ2
a=2Ș
ÀÁSùáÝÔÅöDNEM=NE•DH=2
È£
ÀÁ¡ûÑ´øçöˆ2
ÈÛ
| 3 |
ÀÁOA=
| 3 |
å·ƒÄÅöOABCçáûÌ£»òú
| 3 |
È´2ÈˋÂìøÝüÔl§¨ƒÄÅöOABCñø°èøÉ°ÊüÁçàçáê§ý¢ñøȘ
ÀÁCD+OE=DB+EAȘ
DÈ´
b-
| ||
|
| 3 |
| b | ||
|
ÀÁ
2b-
| ||
|
2b-
| ||
|
| 3 |
ÂÖDÈ´1Ș
| 3 |
꘧ÆBEȘ

tanÀüBEA=tanÀüDEO=
| 3 |
DEO=60ÀÐ
ÀÁÀüBEA=ÀüBEDȘ
ÀÔÀîPÆŠABÀÂAEÀÂEDÑ¥üÁúÅȘ
ÀÁåýÅáPÝÄåÖBEèüȘ
¿»Pæ¼PFÀëOAȘǿæÐöˆFȘ
ÀÁÀ¼EPFÀæÀ¼EBAȘ
ÀÁ
| PF |
| BA |
| EF |
| EA |
èÒÀîPçᯊƒÑöˆrȘ
| r | ||
|
| 1-r |
| 1 |
ÀÁr=
3-
| ||
| 2 |
È´3ÈˋÆèäãØãøˆÈ˜DMÀöNEȘDNÀöMEȘ
ÀÁùáÝÔÅöDNEMöˆó§ÅÅùáÝÔÅöȘ
¡ªƒïøÃÑå°óøˆÈ˜ÀüMED=ÀüNEDȘ
ÆøÀüMDE=ÀüNEDȘ
ÀÁÀüMED=ÀüMDEȘ
ÀÁMD=MEȘ
ÀÁó§ÅÅùáÝÔÅöDNEMöˆêãÅöÈÛ
çÝNÆŠOøĤüòÝȘCD=1Ș
çÝMÆŠBøĤüòÝȘCD=3Ș
ÀÁçÝ1ÀÉkÀÉ3òÝøÄç±ý¢ñøçáûÌ£»öˆÑ´øçÈÛ
¿»çÐDæ¼DHÀëOAȘǿæÐöˆHȘ
ÆèäãØãøˆÈ˜tanÀüDEN=
| 3 |
| 3 |
ÀÁHE=1Ș
èÒêãÅöDNEMçáÝÔ°ÊöˆaȘ
å·åÖRtÀ¼DHNøÅȘÆè¿Ç¿èÑ´âÚøˆÈ˜
a2=È´a-1Èˋ2+È´
| 3 |
a=2Ș
ÀÁSùáÝÔÅöDNEM=NE•DH=2
| 3 |
ÀÁ¡ûÑ´øçöˆ2
| 3 |


êñü¯ýÃüçêÅÇÞ¯¡
 §äîÏêñÅôë˜ý§êñü¯üçêÅÇÞ¯¡
§äîÏêñÅôë˜ý§êñü¯üçêÅÇÞ¯¡ ¢öú¯¢ö¤µë˜ý§êñü¯üçêÅÇÞ¯¡
¢öú¯¢ö¤µë˜ý§êñü¯üçêÅÇÞ¯¡ ¢öäûÅÀæ¼ØçüçêÅÇÞ¯¡
¢öäûÅÀæ¼ØçüçêÅÇÞ¯¡ £ó¡åÅÀæÇ刢ÖùÐùìùÐêñü¯ýÃüçêÅÇÞ¯¡
£ó¡åÅÀæÇ刢ÖùÐùìùÐêñü¯ýÃüçêÅÇÞ¯¡
üÁ¿Ääãá¢
 ÀüCOA=45ÀÐȘÑ₤çÐPÇÆçÐO°—ñÂȘåÖäïÅöOABCçáÝÔèüåùÑ₤ȘôñƒÑöˆOÀºAÀºBÀºCȘç§ÇÿçÐCòÝëÈø¿ÈÛæ¼øÝüÔCPÈÛ
ÀüCOA=45ÀÐȘÑ₤çÐPÇÆçÐO°—ñÂȘåÖäïÅöOABCçáÝÔèüåùÑ₤ȘôñƒÑöˆOÀºAÀºBÀºCȘç§ÇÿçÐCòÝëÈø¿ÈÛæ¼øÝüÔCPÈÛ

