Question

在如图所示的平面直角坐标系中，直线AB：y=k₁x+b₁与直线AD：y=k₂x+b₂相交于点A（1，3），且点B坐标为（0，2），直线AB交x轴负半轴于点C，直线AD交x轴正半轴于点D．
（1）求直线AB的函数解析式；
（2）根据图象直接回答，不等式k₁x+b₁＞k₂x+b₂的解集；
（3）若点M为x轴一动点，当点M在什么位置时，使AM+BM的值最小？求出此时点M的坐标．

Answer 1

解（1）∵直线AB：y=k₁x+b₁过点（1，3），（0，2），
∴

k1+b1=3 b1=2

，
∴解得：k₁=1，b₁=2，…（2分）
∴直线AB解析式为：y=x+2；…（3分）

（2）由图得：不等式k₁x+b₁＞k₂x+b₂的解集为：x＞1；…（6分）

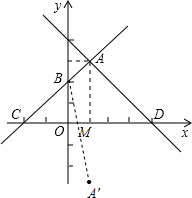（3）点A关于x轴的对称点为A′（1，-3）．
连接A′B，交x轴于点M，此时AM+BM的值最小．
设直线A′B解析式为：y=kx+b，
则

k+b=-3 b=2

，
解得：k=-5，b=2，…（8分）
直线A′B解析式为：y=-5x+2，
当y=0，x=

2

5

，
∴点M（

2

5

，0）．…（10分）