��Ŀ����
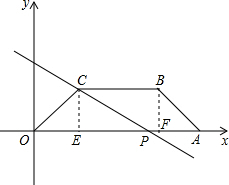
��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OC=AB=4��BC=6�� ��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��
��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��
��1��������OABC�������
��2����ֱ��CP������OABC������ֳ���ȵ�������ʱ����ֱ��CP�Ľ���ʽ��
��3������OCP�ǵ���������ʱ����д����P�����꣨��Ҫ����̣�ֻ��д���������
 ��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��
��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP����1��������OABC�������
��2����ֱ��CP������OABC������ֳ���ȵ�������ʱ����ֱ��CP�Ľ���ʽ��
��3������OCP�ǵ���������ʱ����д����P�����꣨��Ҫ����̣�ֻ��д���������
��1������C��CE��OA��E������B��BF��OA��F��
��CB��OA��
���CEF=��BFE=��ECB=90�㣬
���ı���CEFB�Ǿ��Σ�
��EF=BC=6��BF=CE��
�ߡ�COA=45�㣬
��CE=OE=OC•sin��COE=4��
=2
��
���ı���OABC�ǵ������Σ�
���BAO=��COA=45�㣬
ͬ���ɵã�BF=AF=2
��
��OA=OE+EF+AF=6+4
��
��S����OABC=
��BC+OA��•CE=
����6+6+4
����2
=12
+8��
��2����ֱ��CP������OABC������ֳ���ȵ������֣�
��S��OPC=
S����OABC=6
+4��
��S��OPC=
OP•CE��
��
��OP��2
=6
+4��
��OP=6+2
��
���P��6+2
��0����
�ߵ�C��2
��2
����
��ֱ��CP�Ľ���ʽΪ��y=kx+b��
��
��
��ã�
��
��ֱ��CP�Ľ���ʽΪ��y=-
x+2
+
��
��3���ٵ�P��OA��ʱ��
��OP=OCʱ��OP=4������P������Ϊ��4��0����
��OC=CPʱ����OE=PE=2
��
��OP=4
����P��������4
��0����
��CP=OPʱ��
�ߡ�COA=45�㣬
���PCO=��COA=45�㣬
���OPC=90�㣬
��OP=OC•cos��COA=2
��
���P��������2
��0����
�ڵ�P��AB��ʱ��OP��OB��PC��AC��
��OB=AC��
��OP��PC��
��PC��BC��OC��
��OP��PC��OC��
���ʱ�����ڵ�Pʹ�á�OCP�ǵ��������Σ�
�۵���P��CB��ʱ��
��CP=OC�����P��������2
+4��2
����
���P����������4��0������4
��0������2
��0������2
+4��2
����
��CB��OA��
���CEF=��BFE=��ECB=90�㣬
���ı���CEFB�Ǿ��Σ�
��EF=BC=6��BF=CE��
�ߡ�COA=45�㣬
��CE=OE=OC•sin��COE=4��
| ||
| 2 |
| 2 |
���ı���OABC�ǵ������Σ�
���BAO=��COA=45�㣬
ͬ���ɵã�BF=AF=2
| 2 |
��OA=OE+EF+AF=6+4
| 2 |

��S����OABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
��2����ֱ��CP������OABC������ֳ���ȵ������֣�
��S��OPC=
| 1 |
| 2 |
| 2 |
��S��OPC=
| 1 |
| 2 |
��
| 1 |
| 2 |
| 2 |
| 2 |
��OP=6+2
| 2 |
���P��6+2
| 2 |
�ߵ�C��2
| 2 |
| 2 |
��ֱ��CP�Ľ���ʽΪ��y=kx+b��
��
|
��ã�
|
��ֱ��CP�Ľ���ʽΪ��y=-
| ||
| 3 |
| 2 |
| 4 |
| 3 |
��3���ٵ�P��OA��ʱ��
��OP=OCʱ��OP=4������P������Ϊ��4��0����
��OC=CPʱ����OE=PE=2
| 2 |
��OP=4
| 2 |
| 2 |
��CP=OPʱ��
�ߡ�COA=45�㣬
���PCO=��COA=45�㣬
���OPC=90�㣬
��OP=OC•cos��COA=2
| 2 |
���P��������2
| 2 |
�ڵ�P��AB��ʱ��OP��OB��PC��AC��
��OB=AC��
��OP��PC��
��PC��BC��OC��
��OP��PC��OC��
���ʱ�����ڵ�Pʹ�á�OCP�ǵ��������Σ�
�۵���P��CB��ʱ��
��CP=OC�����P��������2
| 2 |
| 2 |
���P����������4��0������4
| 2 |
| 2 |
| 2 |
| 2 |

��ϰ��ϵ�д�
 ����С״Ԫ��������������ϵ�д�
����С״Ԫ��������������ϵ�д�
�����Ŀ







