题目内容
【题目】如图,△ABC、△DEP是两个全等的等腰直角三角形,∠BAC=∠PDE=90°.
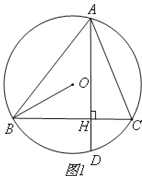
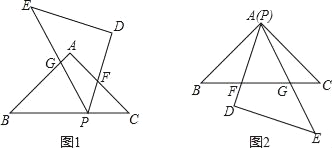
(1)若将△DEP的顶点P放在BC上(如图1),PD、PE分别与AC、AB相交于点F、G.求证:△PBG∽△FCP;
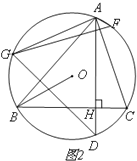
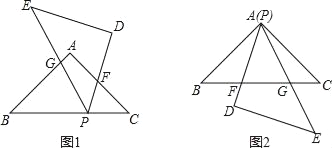
(2)若使△DEP的顶点P与顶点A重合(如图2),PD、PE与BC相交于点F、G.试问△PBG与△FCP还相似吗?为什么?
【答案】(1)证明见解析(2)△PBG与△FCP相似
【解析】试题分析:(1)已知△ABC、△DEP是两个全等的等腰直角三角形,即可得∠B=∠C=∠DPE=45°,∠BPG+∠CPF=135°;在△BPG中,∠B=45°,∠BPG+∠BGP=135°,由此可得∠BGP=∠CPF,再由∠B=∠C,根据两角对应相等的两个三角形相似即可得△PBG∽△FCP;(2)△PBG与△FCP相似,由△ABC、△DEP是两个全等的等腰直角三角形,可得∠B=∠C=∠DPE=45°,又因∠BGP=∠C+∠CPG=45°+∠CAG,∠CPF=∠FPG+∠CAG=45°+∠CAG,所以∠AGP=∠CPF,再由∠B=∠C,根据两角对应相等的两个三角形相似即可得△PBG∽△FCP.
试题解析:
(1)证明:如图1,
∵△ABC、△DEP是两个全等的等腰直角三角形,
∴∠B=∠C=∠DPE=45°,
∴∠BPG+∠CPF=135°,
在△BPG中,∵∠B=45°,
∴∠BPG+∠BGP=135°,
∴∠BGP=∠CPF,
∵∠B=∠C,
∴△PBG∽△FCP;
(2)△PBG与△FCP相似.理由如下:
如图2,∵△ABC、△DEP是两个全等的等腰直角三角形,
∴∠B=∠C=∠DPE=45°,
∵∠BGP=∠C+∠CPG=45°+∠CAG,
∠CPF=∠FPG+∠CAG=45°+∠CAG,
∴∠AGP=∠CPF,
∵∠B=∠C,
∴△PBG∽△FCP.

 习题精选系列答案
习题精选系列答案