题目内容
【题目】如图,长方形纸片ABCD中,AB=6 cm,BC=8 cm,点E是BC边上一点,连接AE,并将△AEB沿AE折叠,得到△AEB′,以C,E,B′为顶点的三角形是直角三角形时,BE的长为____cm.

【答案】3或6
【解析】试题解析:①∠B′EC=90°时,如图1,∠BEB′=90°,
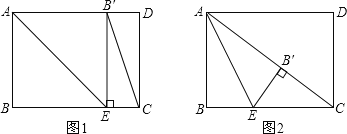
由翻折的性质得∠AEB=∠AEB′=![]() ×90°=45°,
×90°=45°,
∴△ABE是等腰直角三角形,
∴BE=AB=6cm;
②∠EB′C=90°时,如图2,
由翻折的性质∠AB′E=∠B=90°,
∴A、B′、C在同一直线上,
AB′=AB,BE=B′E,
由勾股定理得,AC=![]() =10cm,
=10cm,
∴B′C=10-6=4cm,
设BE=B′E=x,则EC=8-x,
在Rt△B′EC中,B′E2+B′C2=EC2,
即x2+42=(8-x)2,
解得x=3,
即BE=3cm,
综上所述,BE的长为3或6cm.
故答案为:3或6.

练习册系列答案
相关题目
【题目】为增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
每月用气量 | 单价(元/m3) |
不超出80m3的部分 | 2.5 |
超出80m3不超出130m3的部分 | a |
超出130m3的部分 | a+0.5 |
(1)若甲用户3月份用气125m3,缴费335元,求a的值;
(2)在(1)的条件下,若乙用户3月份缴费392元,则乙用户3月份的用气量是多少?