题目内容
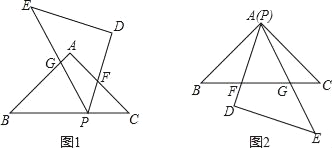
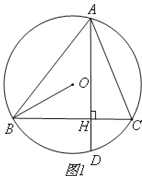
【题目】如图,△ABC内接于⊙O,弦AD⊥BC,垂足为H,连接OB.
(1)如图1,求证:∠DAC=∠ABO;
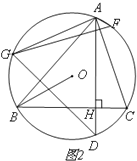
(2)如图2,在弧AC上取点F,使∠CAF=∠BAD,在弧AB取点G,使AG∥OB,若∠BAC=600,
求证:GF=GD;
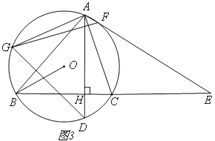
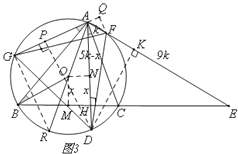
(3)如图3,在(2)的条件下,AF、BC的延长线相交于点E,若AF:FE=1:9,求sin∠ADG的值。
【答案】(1)详见解析;(2)详见解析;(3)![]() .
.
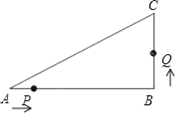
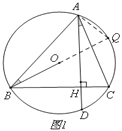
【解析】试题分析:(1)延长BO交⊙O于点Q,连接AQ.由圆周角定理可得:∠AQB=∠ACB,再由等角的余角相等即可得出结论;
(2)证明△DFG是等边三角形即可;
(3)延长GA,作FQ⊥AG,垂足为Q,作ON⊥AD,垂足为N,作OM⊥BC,垂足为M,延长AO交⊙O于点R,连接GR.作DP⊥AG,DK⊥AE,垂足为P、K.设AF=k,则FE=9k,AE=10k.在△AHE中, AH=5k.设NH=x,则AN=5k-x, AD=10k-2x.在△AQF中, AF=k,AQ=![]() ,FQ=
,FQ=![]() k.由(2)知:△GDF是等边三角形,得到GD=GF=DF,进而得到AG=9k-2x.
k.由(2)知:△GDF是等边三角形,得到GD=GF=DF,进而得到AG=9k-2x.
OM=NH=x,BC=![]() x, GF=BC=
x, GF=BC=![]() x.在△GQF中,GQ=AG+AQ=
x.在△GQF中,GQ=AG+AQ=![]() k-2x,QF=
k-2x,QF=![]() k,GF=
k,GF=![]() x,由勾股定理解出
x,由勾股定理解出![]() ,得到AG=9k-2x=
,得到AG=9k-2x= ![]() ,AR=2OB=4OM=4x=7k.在△GAR中,由sin∠ADG=sin∠R即可得出结论.
,AR=2OB=4OM=4x=7k.在△GAR中,由sin∠ADG=sin∠R即可得出结论.
试题解析:解:(1)证明:如图1,延长BO交⊙O于点Q,连接AQ.
∵BQ是⊙O直径,∴∠QAB=900.∵AD⊥BC,∴∠AHC=900.
∵弧AB=弧AB,∴∠AQB=∠ACB.
∵∠AQB+∠ABO=900,∠ACB+∠CAD=900
∴∠ABO=∠CAD
(2)证明:如图2,连接DF.

∵AG∥OB,∴∠ABO=∠BAG.∵∠ABO=∠CAD,∴∠CAD=∠BAG.
∵∠BAC=600,∴∠BAD+∠CAD=∠BAD+∠BAG=600,即∠GAD=∠BAC=60°.∵∠BAD=∠CAF.∴∠CAF+∠CAD=600,∴∠GAD=∠DAF=600,∴∠DGF=∠DAF=60°.
∵弧GD=弧GD,∴∠GAD=∠GFD=600,∴∠GFD=∠DGF=600,∴△DFG是等边三角形,∴GD=GF.
(3)如图3,
延长GA,作FQ⊥AG,垂足为Q,作ON⊥AD,垂足为N,作OM⊥BC,垂足为M,延长AO交⊙O于点R,连接GR.作DP⊥AG,DK⊥AE,垂足为P、K.
∵AF:FE=1:9,∴设AF=k,则FE=9k,AE=10k.在△AHE中,∠E=300,∴AH=5k.
设NH=x,则AN=5k-x.∵ON⊥AD,∴AD=2AN=10k-2x
又在△AQF中,∵∠GAF=1200,∴∠QAF=600,AF=k,∴AQ=![]() ,FQ=
,FQ=![]() k.
k.
由(2)知:△GDF是等边三角形,∴GD=GF=DF,
∵∠GAD=∠DAF=600,∴DP=DK,∴△GPD≌△FKD,△APD≌△AKD
∴FK=GP,AP=AK,∠ADK=300,∴AD=2AK=AP+AK=AF+AG
∴AG=10k-2x-k=9k-2x.
∵作OM⊥BC,ON⊥AD,∴OM=NH=x.∵∠BOD=![]() ∠BOC=∠BAC=600
∠BOC=∠BAC=600
∴BC=2BM=![]() x.∵∠BOC=∠GOF,∴GF=BC=
x.∵∠BOC=∠GOF,∴GF=BC=![]() x
x
在△GQF中,GQ=AG+AQ=![]() k-2x,QF=
k-2x,QF=![]() k,GF=
k,GF=![]() x
x
∵![]()
∴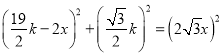 ,
,
![]() .
.
∴AG=9k-2x= ![]() ,AR=2OB=4OM=4x=7k,
,AR=2OB=4OM=4x=7k,
在△GAR中,∠RGA=900,
∴sin∠ADG=sin∠R=![]() =
=![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭.小明家中买了一辆小轿车,他连续记录了7天中每天行驶的路程(如表),以50km为标准,多于50km的记为“+”,不足50km的记为“﹣”,刚好50km的记为“0”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程(km) | ﹣8 | ﹣11 | ﹣14 | 0 | ﹣16 | +41 | +8 |
(1)请求出这七天平均每天行驶多少千米;
(2)若每行驶100km需用汽油6升,汽油价6.2元/升,请估计小明家一个月(按30天计)的汽油费用是多少元?