题目内容
【题目】某中学八年级学生在学习等腰三角形的相关知识时时,经历了以下学习过程:
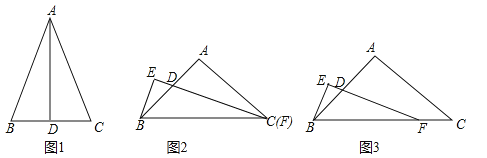
(1)(探究发现)如图1,在![]() 中,若
中,若![]() 平分
平分![]() ,
,![]() 时,可以得出
时,可以得出![]() ,
,![]() 为
为![]() 中点,请用所学知识证明此结论.
中点,请用所学知识证明此结论.
(2)(学以致用)如果![]() 和等腰
和等腰![]() 有一个公共的顶点
有一个公共的顶点![]() ,如图2,若顶点
,如图2,若顶点![]() 与顶点
与顶点![]() 也重合,且
也重合,且![]() ,试探究线段
,试探究线段![]() 和
和![]() 的数量关系,并证明.
的数量关系,并证明.
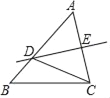
(3)(拓展应用)如图3,在(2)的前提下,若顶点![]() 与顶点
与顶点![]() 不重合,
不重合,![]() ,(2)中的结论还成立吗?证明你的结论
,(2)中的结论还成立吗?证明你的结论
【答案】(1)详见详解;(2)DF=2BE,证明详见详解;(3)DF=2BE,证明详见详解
【解析】
(1)只要证明△ADB≌△ADC(ASA)即可;
(2)如图2中,延长BE交CA的延长线于K,只要证明△BAK≌△CAD(ASA)即可;
(3)作FK∥CA交BE的延长线于K,交AB于J,利用(2)中的结论证明即可.
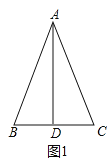
解:(1)如图1中,∵AD⊥BC,∴∠ADB=∠ADC=90°,
∵DA平分∠BAC,∴∠DAB=∠DAC,
∵AD=AD,∴△ADB≌△ADC(ASA),
∴AB=AC,BD=DC.
(2)结论:DF=2BE.
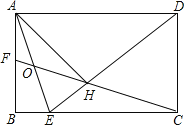
理由:如图2中,延长BE交CA的延长线于K.

∵CE平分∠BCK,CE⊥BK,
∴由(1)中结论可知:CB=CK,BE=KE,
∵∠BAK=∠CAD=∠CEK=90°,
∴∠ABK+∠K=90°,∠ACE+∠K=90°,
∴∠ABK=∠ACD,∵AB=AC,
∴△BAK≌△CAD(ASA),CD=BK,
∴CD=2BE,
即DF=2BE.
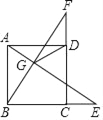
(3)如图3中,结论不变:DF=2BE.
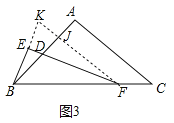
理由:作FK∥CA交BE的延长线于K,交AB于J.
∵FK∥AC,∴∠FJB=∠A=90°,∠BFK=∠BCA,
由(2)可知Rt△ABC为等腰三角形
∵∠JBF=45°,
∴△BJF是等腰直角三角形,
∵∠BFE=![]() ∠ACB,∴∠BFE=
∠ACB,∴∠BFE=![]() ∠BFJ,
∠BFJ,
由(2)可知:DF=2BE.

 阅读快车系列答案
阅读快车系列答案