题目内容
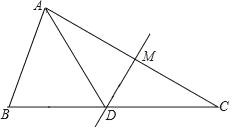
【题目】如图,在正方形ABCD中,BC=2,E、F分别为射线BC,CD上两个动点,且满足BE=CF,设AE,BF交于点G,连接DG,则DG的最小值为_______.
【答案】![]() ﹣1
﹣1
【解析】
先由图形确定:当O、G、D共线时,DG最小;根据正方形的性质证明△ABE≌△BCF(SAS),可得∠AGB=90°,利用勾股定理可得OD的长,从而得DG的最小值.
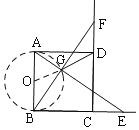
在正方形ABCD中,AB=BC,∠ABC=∠BCD,
在△ABE和△BCF中,
 ,
,
∴△ABE≌△BCF(SAS),
∴∠BAE=∠CBF,
∵∠CBF+∠ABF=90°
∴∠BAE+∠ABF=90°
∴∠AGB=90°
∴点G在以AB为直径的圆上,
由图形可知:当O、G、D在同一直线上时,DG有最小值,如图所示:
∵正方形ABCD,BC=2,
∴AO=1=OG
∴OD=![]() ,
,
∴DG=![]() 1,
1,
故答案为:![]() 1.
1.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
【题目】某水果基地计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果).如表为装运甲、乙、丙三种水果的重量及利润.
甲 | 乙 | 丙 | |
每辆汽车能装的数量(吨) | 4 | 2 | 3 |
每吨水果可获利润(千元) | 5 | 7 | 4 |
(1)用8辆汽车装运乙、丙两种水果共22吨到A地销售,问装运乙、丙两种水果的汽车各多少辆?
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用m表示)
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?