题目内容
【题目】在平面直角坐标系中,点A、C的坐标分别是(﹣1,0)和(2,0),以OC为直径作圆⊙P,AB切⊙P于点B,交y轴于点E.点M是劣弧![]() 上一动点,CM交BP于点N,BM交x轴于点D.
上一动点,CM交BP于点N,BM交x轴于点D.
(1)求点E的坐标;
(2)当点M在弧BO上运动时,PD﹣PN的值是否变化?为什么?
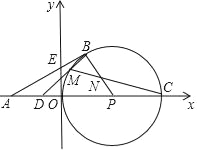
【答案】(1)E(0,![]() );(2)PD﹣PN 值不变,理由见解析
);(2)PD﹣PN 值不变,理由见解析
【解析】
(1) 根据切线的性质和直角三角形的边关系解答即可;
(2) 连接OB,根据等边三角形的性质和全等三角形的判定与性质得出OD=PN, 进而解答即可.
(1)∵A(﹣1,0),C(2,0),
∴OA=1,OC=2,
∵以OC为直径作⊙P,
∴OP=PC=![]() OC=1=OA,
OC=1=OA,
∴AP=2,
∵AB切⊙P于点B,
∴∠APB=90°,BP=OP=1,
∴BP=![]() AP,
AP,
则在直角△ABP中,∠BAP=30°,
∴直角△AEO中,OE=![]() ,
,
∴E(0,![]() )
)
(2)判断:PD﹣PN 值不变,
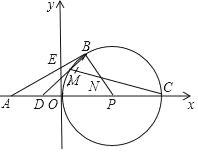
理由:连接OB,由(1)可知∠APB=90°,BP=![]() AP,则∠BAP=30°,∠APB=60°,
AP,则∠BAP=30°,∠APB=60°,
∵BP=OP,
∴△OBP为等边三角形,
∴OB=BP=PC,∠BOP=∠BPO=60°,
∵∠BOD+∠BOP=∠BPO+∠CPN,
∴∠BOD=∠CPN,
∵∠OBM与∠OCM为同![]() 所对的圆周角,
所对的圆周角,
∴∠OBM=∠OCM,
在△OBD与△PCN中, ,
,
∴△OBD≌△PCN(ASA),
∴OD=PN,
∴PD﹣PN=PD﹣OD=PO=1,
∴PD﹣PN 值不变.

练习册系列答案
相关题目