题目内容
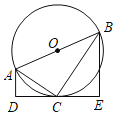
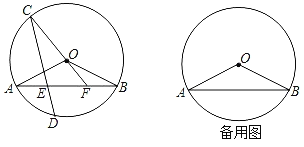
【题目】如图,已知⊙O为△ABC的外接圆,AC为直径,且AC=2![]() .
.
(1)用尺规作图作出∠ABE=45°,与弧AC交于E点(保留作图痕迹,不写作法);
(2)若∠A=30°,求BE的长.
【答案】(1)见解析;(2)BE=1+![]() .
.
【解析】
(1)首先根据直径所对的圆周角为90°可知∠ABC=90°,由此可知要使∠ABE为45°,只要画出∠ABC的角平分线即可,据此按照角平分线的作图方法画图即可;
(2)过点C作CF⊥BE,垂足为F,连接CE,首先根据AC为直径得出∠ABC=90°,然后利用“30°角所对的直角边为斜边一半”得出BC的长,然后在Rt△BFC中利用三角函数求出CF,由此进一步得出BF,最后在Rt△EFC中再次根据三角函数求出EF,由此即可得出答案.
(1)如图,∠ABE即为所求;
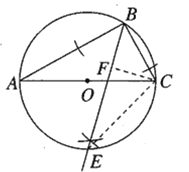
(2)过点C作CF⊥BE,垂足为F,连接CE,
∵∠A=30°,
∴∠BEC=30°,
∵AC为直径,
∴∠ABC=90°,
由(1)可知∠ABE=45°,
∴∠EBC=45°,
在Rt△ABC中,∵∠A=30°,AC=![]() ,
,
∴BC=![]() ,
,
在Rt△BFC中,sin∠FBC=![]() ,
,
∴CF=1,
∵∠EBC=45°,CF⊥BE,
∴∠BCF=45°,
∴BF=CF=1,
在Rt△EFC中,tan∠BEC=![]() ,
,
∴EF=![]() ,
,
∴BE=BF+EF=![]() .
.

练习册系列答案
相关题目