题目内容
【题目】如图,OC是∠AOM的平分线,OD是∠BOM的平分线.
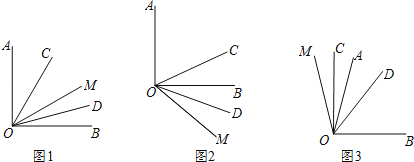
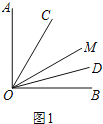
(1)如图1,若∠AOB=90°,∠AOM=60°,求∠COD的度数;
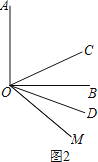
(2)如图2,若∠AOB=90°,∠AOM=130°,则∠COD= °;
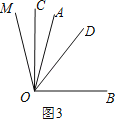
(3)如图3,若∠AOB=m°,∠AOM=n°,则∠COD= °.
【答案】(1)45°;(2)45;(3)![]() (m﹣n)°.
(m﹣n)°.
【解析】
试题分析:(1)直接利用角平分线的性质分别得出∠COM和∠DOM的值,进而得出答案;
(2)直接利用角平分线的性质分别得出∠COM和∠DOM的值,进而得出答案;
(3)直接利用角平分线的性质分别得出∠COM和∠DOM的值,进而得出答案.
解:(1)如图1,∵∠AOB=90°,∠AOM=60°,
∴∠BOM=∠AOB﹣∠AOM=90°﹣60°=30°,
∵OC是∠AOM的平分线,OD是∠BOM的平分线,
∴∠COM=![]() ∠AOM=
∠AOM=![]() ×60°=30°,
×60°=30°,
∠DOM=![]() ∠BOM=
∠BOM=![]() ×30°=15°,
×30°=15°,
∴∠COD=∠COM+∠DOM=30°+15°=45°;
(2)如图2,∵∠AOB=90°,∠AOM=130°,
∴∠BOM=∠AOM﹣∠AOB=130°﹣90°=40°,
∵OC是∠AOM的平分线,OD是∠BOM的平分线,
∴∠COM=![]() ∠AOM=
∠AOM=![]() ×130°=65°,
×130°=65°,
∠DOM=![]() ∠BOM=
∠BOM=![]() ×40°=20°,
×40°=20°,
∴∠COD=∠COM﹣∠DOM=65°﹣20°=45°
故答案为:45.
(3)如图3,∵∠AOB=m°,∠AOM=n°,
∴∠BOM=∠AOB+∠AOM=m°+n°,
∵OC是∠AOM的平分线,OD是∠BOM的平分线,
∴∠COM=![]() ∠AOM=
∠AOM=![]() ×n°=
×n°=![]() n°,
n°,
∠DOM=![]() ∠BOM=
∠BOM=![]() m°,
m°,
∴∠COD=∠DOM﹣∠COM=![]() m°﹣
m°﹣![]() n°=
n°=![]() (m﹣n)°.
(m﹣n)°.
故答案为:![]() (m﹣n)°.
(m﹣n)°.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目