题目内容
如图,已知在△ABC中,AB=AC,BC在直线MN上.
(1)根据下列要求补完整图形,
①画出△ABC关于直线MN对称的三角形A′BC;
②在线段BC上取两点D、E(BD<
BC,BD<
BC),使BD=CE,连接AD、AE、A′D、A′E;
(2)求证:四边形ADA′E是菱形.

(1)根据下列要求补完整图形,
①画出△ABC关于直线MN对称的三角形A′BC;
②在线段BC上取两点D、E(BD<
| 1 |
| 2 |
| 1 |
| 2 |
(2)求证:四边形ADA′E是菱形.

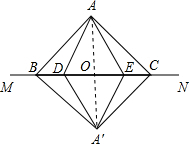
(1)所画图形如下所示:
(2)说明:连接AA′,交MN于O,
∵MN是对称轴,
∴MN垂直平分AA′
又∵AB=AC
∴AA′垂直平分BC,
又∵BD=CE
∴DO=EO.
即 AA′垂直平分DE,
∴AA′与DE互相垂直平分,
∴四边形ADA′E是菱形.
(2)说明:连接AA′,交MN于O,
∵MN是对称轴,
∴MN垂直平分AA′
又∵AB=AC
∴AA′垂直平分BC,
又∵BD=CE
∴DO=EO.
即 AA′垂直平分DE,
∴AA′与DE互相垂直平分,
∴四边形ADA′E是菱形.


练习册系列答案
相关题目


 长度的速度沿y轴正方向运动,设D、E两点的运动时间为t秒.
长度的速度沿y轴正方向运动,设D、E两点的运动时间为t秒.





