题目内容

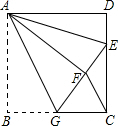
已知：矩形ABCD中，AB=6，AD=8，将矩形顶点B沿GF折叠，使B落在AD上（不与A、D重合）的E处，点G、F分别在AB、BC上．
（1）不论点E在何处，试判断△BFE的形状；
（2）若AG：GB=1：2时，求证：EG平分∠AEB；
（3）若
AG
GB
=
1
4
，试求BF的长．
（1）证明：∵矩形顶点B沿GF折叠B落在AD上（不与A、D重合）的E处，
∴BF=EF，
∴△BEF是等腰三角形；

（2）证明：∵AG：GB=1：2，AB=6，
∴AG=6×
1
1+2
=2，GB=6×
2
1+2
=4，
由翻折性质，EG=BG=4，
在Rt△AGE中，AE=
EG2-AG2
=
42-22
=2
3
，
∴
AG
AE
=
2
2
3
=
3
3
，
AE
AB
=
2
3
6
=
3
3
，
∴
AG
AE
=
AE
AB
，
又∵∠A=∠A，
∴△ABE∽△AEG，
∴∠AEG=∠ABE，
由EG=BF得，∠ABE=∠BEG，
∴∠AEG=∠BEG，
∴EG平分∠AEB；

（3）∵
AG
GB
=
1
4
，AB=6，
∴AG=6×
1
1+4
=
6
5
，BG=6×
4
1+4
=
24
5
，
由翻折性质，EG=BG=
24
5
，
在Rt△AGE中，AE=
EG2-AG2
=
(
24
5
)2-(
6
5
)2
=
6
15
5
，
由翻折的性质，∠EBF+∠BFG=90°，
∵∠ABE+∠EBF=∠ABC=90°，
∴∠ABE=∠BFG，
又∵∠A=∠ABF=90°，
∴△ABE∽△BFG，
∴
AE
BG
=
AB
BF
，
即
6
15
5
24
5
=
6
BF
，
解得BF=
8
15
5
．
练习册系列答案
相关题目
认真画一画．如图，在正方形网格上有一个△DEF．
（1）作△DEF关于直线HG的轴对称图形△D′E′F′（不写作法）；
（2）作EF边上的高（不写作法）；
（3）若网格上的最小正方形边长为1，则△DEF的面积为______．
如图，正方形纸片ABCD的边长为3，点E、F分别在边BC、CD上，将AB、AD分别和AE、AF折叠，点B、D恰好都将在点G处，已知BE=1，则EF的长为（　　）
A．
3
2
B．
5
2
C．
9
4
D．3
如图，点A和点B相距60cm，且关于直线L对称，一只电动青蛙在与直线L相距20cm，与点A相距50cm的点P1处以A为对称中心跳至P2处，然后从P2处以L为对称轴跳至P3处，再从P3处以B为对称中心跳至P4处，再从P4处以L为对称轴跳至P5处，又从P5处以A为对称中心跳至P6处…，如此重复跳跃，则P2011与直线L的距离是（　　）
A．20cmB．30cmC．40cmD．50cm
下列图形中，既是轴对称图形又是中心对称图形的是（　　）
A．菱形、正方形、平行四边形
B．矩形、等腰三角形、圆
C．矩形、正方形、等腰梯形
D．菱形、正方形、圆
如图，正方形ABCD中，AB=6，点G是边BC的中点，连接AG．将△ABC沿AG对折至△AFG，延长GF交边CD于点E，连接AE、CF．下列结论：①△AFE≌△ADE；②EC=2DE；③S△EFC=2；④∠BAG+∠AFC=180°．其中正确结论的个数是（　　）
A．1B．2C．3D．4
已知：如图，已知△ABC，
（1）画出与△ABC关于x轴对称的图形△A1B1C1．
（2）求△ABC的面积．
如图，已知在△ABC中，AB=AC，BC在直线MN上．
（1）根据下列要求补完整图形，
①画出△ABC关于直线MN对称的三角形A′BC；
②在线段BC上取两点D、E（BD＜
1
2
BC，BD＜
1
2
BC），使BD=CE，连接AD、AE、A′D、A′E；
（2）求证：四边形ADA′E是菱形．
如图，四边形ABCD是矩形，AB：AD=4：3，把矩形沿直线AC折叠，点B落在点E处，连接DE，则DE：AC=______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网