题目内容
【题目】在正方形ABCD中,DE为正方形的外角∠ADF的角平分线,点G在线段AD上,过点G作PG⊥DE于点P,连接CP,过点D作DQ⊥PC于点Q,交射线PG于点H.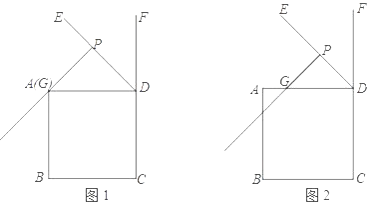
(1)如图1,若点G与点A重合.
①依题意补全图1;
②判断DH与PC的数量关系并加以证明;
(2)如图2,若点H恰好在线段AB上,正方形ABCD的边长为1,请写出求DP长的思路(可以不写出计算结果).
【答案】
(1)解:①依题意补全图1,如图1所示:
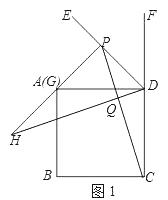
②DH=PC,理由如下:
∵DE为正方形的外角∠ADF的角平分线,
∴∠EDF=∠ADE=45°,
∵PG⊥DE于点P,
∴∠DAP=45°,
∴∠HAD=135°,∠PDC=135°,
∴∠HAD=∠PDC,
∵四边形ABCD为正方形,
∴AD=CD,
∵DQ⊥PC,
∴∠CDQ+∠DCQ=90°,
∵∠ADQ+∠CDQ=90°,
∴∠ADQ=∠DCQ,
在△HAD和△PDC中,
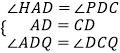 ,
,
∴△HAD≌△PDC(ASA),
∴DH=CP
(2)解:求DP长的思路如下:如图2所示:
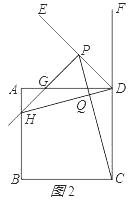
a、与②同理得:∠HGD=∠PDC,∠ADQ=∠DCP,
∴△HGD∽△PDC;
b、由②可知△GPD为等腰直角三角形,
∴∠AGH=∠PGD=45°,
∴△AGH为等腰直角三角形,
设DP=PG=x,则GD= ![]() x,AG=1﹣
x,AG=1﹣ ![]() x,GH=
x,GH= ![]() ﹣2x;
﹣2x;
c、由△HGD∽△PDC得: ![]() ,
,
即 ![]() ,
,
解得:x= ![]() (负值舍去),
(负值舍去),
∴DP= ![]()
【解析】(1)①依题意补全图形即可。
②由正方形的性质和角平分线得出∠EDF=∠ADE=45°,再证出∠HAD=∠PDC,∠ADQ=∠DCQ,根据ASA证明△HAD≌△PDC,得出对应边相等即可。
(2)思路如下:a、与②同理可证∠HGD=∠PDC,∠ADQ=∠DCP,可证△HGD∽△PDC;b、由②可知△GPD为等腰直角三角形,根据已知条件易证△AGH为等腰直角三角形,可设DP=PG=x,用含x的代数式分别表示出GD、AG、GH的长。c、由△HGD∽△PDC得出比例式,解方程即可求得DP的长。
【考点精析】掌握角的平分线和正方形的性质是解答本题的根本,需要知道从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案