题目内容
如图，在△ABC中，A、B两点关于直线DE对称；A、C两点关于直线DF对称，DE交AB于点E，交BC于点D；DF交AC于点F．
（1）试说明BD=CD；
（2）试判断四边形AEDF的形状，并说明理由．
（1）试说明BD=CD；
（2）试判断四边形AEDF的形状，并说明理由．
（1）连接AD，
∵A、B两点关于直线DE对称，
∴BD=AD，
∵A、C两点关于直线DF对称，
∴CD=AD，
∴BD=CD．
（2）四边形AEDF是矩形．
理由是：∵D、E、F分别为BC、AB、AC的中点，
∴DE∥AC，DF∥AB，
∴四边形AEDF是平行四边形，
∵A、B两点关于直线DE对称，
∴∠AED=90°，
∴平行四边形AEDF是矩形．
∵A、B两点关于直线DE对称，
∴BD=AD，
∵A、C两点关于直线DF对称，
∴CD=AD，
∴BD=CD．
（2）四边形AEDF是矩形．
理由是：∵D、E、F分别为BC、AB、AC的中点，
∴DE∥AC，DF∥AB，
∴四边形AEDF是平行四边形，
∵A、B两点关于直线DE对称，
∴∠AED=90°，
∴平行四边形AEDF是矩形．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
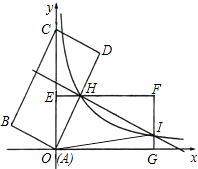
于点H，交AD于点G．